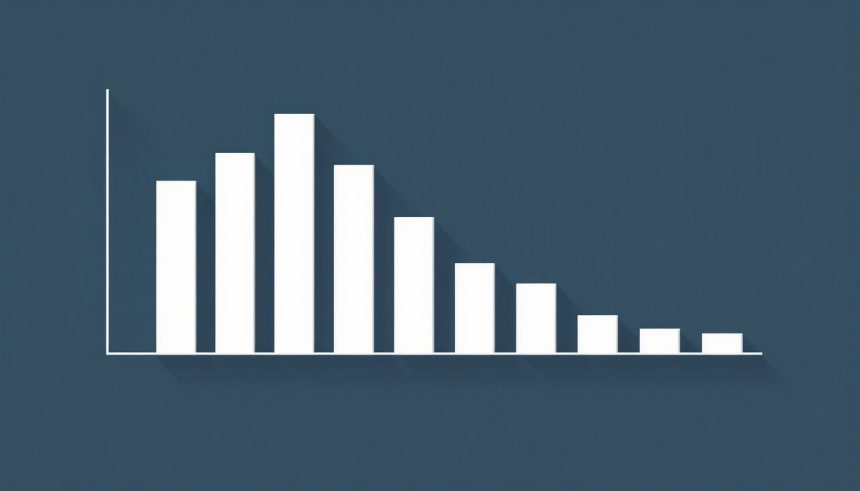
A Zipf-törvény egy empirikus statisztikai eloszlás, ami meglepően sok területen felbukkan, a nyelvészettől a populációbiológiáig. Lényege, hogy egy adathalmazban a leggyakoribb elem körülbelül kétszer olyan gyakori, mint a második leggyakoribb, háromszor olyan gyakori, mint a harmadik, és így tovább. Ez a hatványtörvény jellegzetes formája.
Az egyik legismertebb példa a szavak gyakorisága egy szövegben. Ha egy hosszabb szöveget vizsgálunk, a leggyakoribb szó (általában egy névelő vagy kötőszó) sokkal gyakrabban fordul elő, mint a második leggyakoribb, és ez a különbség exponenciálisan csökken a ritkább szavak felé haladva. Hasonló mintázat figyelhető meg a városok népességének eloszlásában, a weboldalak látogatottságában, és még a cégméretek eloszlásában is.
A Zipf-törvény elterjedtsége arra utal, hogy valamilyen mélyebb, univerzális mechanizmus húzódik meg a háttérben, ami a komplex rendszerek viselkedését szabályozza.
Számos elmélet létezik a törvény magyarázatára. Az egyik legelterjedtebb a „legkisebb erőfeszítés elve”, ami szerint a rendszerek (legyen az egy nyelv, egy gazdaság vagy egy ökoszisztéma) hajlamosak arra, hogy a lehető legkevesebb erőfeszítéssel érjék el a céljukat. Ez a törekvés vezethet az erőforrások koncentrációjához néhány domináns elemben, ami a Zipf-törvény szerinti eloszlást eredményezi.
Egy másik magyarázat a preferenciális kapcsolódás elve, ami azt mondja ki, hogy az új elemek nagyobb valószínűséggel kapcsolódnak a már népszerű elemekhez. Ez a jelenség a hálózatok növekedésében figyelhető meg, és szintén hatványtörvény szerinti eloszláshoz vezethet. A Zipf-törvény tehát nem csupán egy furcsa statisztikai anomália, hanem egy fontos betekintést nyújt a komplex rendszerek működésébe.
A Zipf-törvény definíciója és matematikai leírása
A Zipf-törvény egy empirikus megfigyelés, amely számos jelenségben megfigyelhető, különösen a természetes nyelvekben és más, nagyméretű adathalmazokban. A törvény lényege, hogy egy adott jelenség gyakorisága fordítottan arányos annak rangsorával. Más szavakkal, a leggyakoribb elem sokkal gyakoribb, mint a második leggyakoribb, a második leggyakoribb sokkal gyakoribb, mint a harmadik, és így tovább.
A matematikai megfogalmazása a következőképpen történik: ha az elemeket a gyakoriságuk alapján csökkenő sorrendbe rendezzük, akkor az n-edik leggyakoribb elem gyakorisága (f(n)) hozzávetőlegesen arányos 1/n-nel. Ezt a következő képlettel fejezhetjük ki:
f(n) ≈ 1 / ns
Ahol:
- f(n) az n-edik leggyakoribb elem gyakorisága.
- n az elem rangsora a gyakorisági sorrendben.
- s egy kitevő, amely a legtöbb természetes jelenségben közel 1 (gyakran 1 körüli érték). Ez az érték a jelenségtől függően változhat.
Például, ha s = 1, akkor a leggyakoribb szó (n = 1) gyakorisága körülbelül kétszerese a második leggyakoribb szó (n = 2) gyakoriságának, és háromszorosa a harmadik leggyakoribb szó (n = 3) gyakoriságának.
A Zipf-törvény nem csak a szavak gyakoriságára vonatkozik. Megfigyelhető más jelenségekben is, például:
- Népességek városokban (a legnagyobb város sokkal nagyobb, mint a második legnagyobb).
- Céges méretek (a legnagyobb cég sokkal nagyobb, mint a második legnagyobb).
- Weboldalakra mutató hivatkozások száma (a legnépszerűbb weboldalra sokkal több hivatkozás mutat, mint a második legnépszerűbbre).
A Zipf-törvény egy hatványtörvény, ami azt jelenti, hogy a gyakoriság és a rangsor közötti kapcsolat nem lineáris. Ez a fajta eloszlás gyakran megfigyelhető komplex rendszerekben, ahol sok kis interakció eredményezi a végső eloszlást. A pontos okok, amiért a Zipf-törvény ilyen széles körben elterjedt, még mindig kutatás tárgyát képezik, de valószínűleg az önoptimalizáló rendszerek és a véletlen növekedés kombinációjának köszönhető.
Bár a Zipf-törvény egy hasznos közelítés, nem tökéletes leírása a valós adatoknak. Gyakran megfigyelhetők eltérések a törvénytől, különösen a szélsőséges értékeknél (a leggyakoribb és a legritkább elemeknél). Mindazonáltal a törvény egy fontos eszköz a nagy adathalmazok elemzéséhez és a komplex rendszerek viselkedésének megértéséhez.
A Zipf-törvény eredete: George Kingsley Zipf és a minimális erőfeszítés elve
A Zipf-törvény az empirikus statisztikai eloszlások egyik legismertebb példája, melyet George Kingsley Zipf amerikai nyelvész és filológus fedezett fel a 20. század közepén. Zipf eredetileg a szavak gyakoriságát vizsgálta egy adott szövegkorpuszban, és azt találta, hogy a szavak gyakorisága fordítottan arányos a rangsorukkal.
Zipf nem csupán a szavak gyakoriságát vizsgálta, hanem megpróbálta megmagyarázni ezt a különös eloszlást. Elméletének központi eleme a minimális erőfeszítés elve. Eszerint mind a beszélő (vagy író), mind a hallgató (vagy olvasó) a lehető legkevesebb energiát szeretné befektetni a kommunikációba.
A beszélő (vagy író) a változatosságra törekszik, hogy minél kevesebb szót kelljen használnia, a hallgató (vagy olvasó) pedig a megszokott, gyakori szavakat preferálja, hogy könnyebben megértse a mondanivalót.
Ez a két ellentétes törekvés – a beszélő egyszerűsítésre való igénye és a hallgató érthetőségre való igénye – egyfajta egyensúlyi állapotot hoz létre, mely a Zipf-törvényben tükröződik. A leggyakoribb szavak rövid, könnyen használható szavak lesznek, míg a ritkább szavak specifikusabbak és pontosabbak, de ritkábban használatosak. Zipf szerint ez az elv nem csak a nyelvre, hanem más rendszerekre is alkalmazható, ahol hasonló erőfeszítés-minimalizálási törekvések jelennek meg.
Bár a Zipf-törvény pontos okai továbbra is vita tárgyát képezik, Zipf minimális erőfeszítés elve egy fontos szempontot kínál a statisztikai eloszlások megértéséhez, és rámutat arra, hogy a rendszer résztvevőinek törekvései hogyan befolyásolják a rendszer egészének jellemzőit.
A Zipf-törvény megjelenése a természetes nyelvben: Szavak gyakorisága és rangsorolása
A Zipf-törvény egy empirikus megfigyelés, amely számos jelenségben megjelenik, de talán leginkább a természetes nyelvekben feltűnő. A törvény azt állítja, hogy egy adott korpuszban (szöveggyűjteményben) a szavak gyakorisága fordítottan arányos a rangsorukkal a gyakorisági listán. Ez azt jelenti, hogy a leggyakoribb szó sokkal többször fordul elő, mint a második leggyakoribb, a második leggyakoribb pedig sokkal többször, mint a harmadik, és így tovább.
Gyakorlatban ez azt jelenti, hogy ha a leggyakoribb szó n-szer fordul elő, akkor a második leggyakoribb szó körülbelül n/2-szer, a harmadik n/3-szor fordul elő. A törvény nem tökéletes, és a pontos arányok a korpusztól függően változhatnak, de a tendencia általában megfigyelhető.
A Zipf-törvény szerint a nyelvben a néhány gyakori szó dominál, míg sok szó ritkán fordul elő.
Ennek a jelenségnek számos következménye van a nyelvészetben és a számítógépes nyelvészetben. Például, a Zipf-törvény segíthet a szövegtömörítésben, mivel a gyakori szavakat rövidebb kódokkal lehet ábrázolni. Továbbá, a törvény felhasználható a nyelvi modellek fejlesztésére, amelyek a szavak előfordulási valószínűségét becsülik meg.
Érdekes módon, a Zipf-törvény nem csak a szavak gyakoriságára vonatkozik, hanem más nyelvi elemekre is, mint például a betűk vagy a hangok eloszlására. Sőt, a törvény más területeken is megfigyelhető, például a városok népességében vagy a weboldalak látogatottságában.
Bár a Zipf-törvény széles körben megfigyelhető, az okai még mindig vitatottak. Számos elmélet létezik, amelyek megpróbálják megmagyarázni a jelenséget, például a legkisebb erőfeszítés elve, amely szerint a beszélők és írók arra törekednek, hogy a lehető legkevesebb erőfeszítéssel kommunikáljanak.
A Zipf-törvény alkalmazása a számítógépes nyelvészetben és a szövegbányászatban
A Zipf-törvény jelentős szerepet játszik a számítógépes nyelvészetben és a szövegbányászatban, mivel leírja a szavak gyakoriságának eloszlását egy adott korpuszban. A törvény azt állítja, hogy a leggyakoribb szó körülbelül kétszer olyan gyakori, mint a második leggyakoribb, háromszor olyan gyakori, mint a harmadik leggyakoribb, és így tovább. Ez az egyszerű, mégis erőteljes összefüggés számos alkalmazást tesz lehetővé.
A szövegbányászatban a Zipf-törvény segíthet a szavak fontosságának megítélésében. Bár a leggyakoribb szavak (pl. névelők, kötőszavak) ritkán hordoznak jelentős tartalmi információt, az eloszlásuk elemzése lehetővé teszi a kevésbé gyakori, de relevánsabb szavak azonosítását. Ez különösen fontos a kulcsszavak kinyerésében és a dokumentumok tartalmának tömör összefoglalásában.
A számítógépes nyelvészetben a Zipf-törvény a nyelvi modellek fejlesztésében is felhasználható. A szavak gyakoriságának ismerete segít a modelleknek abban, hogy jobban megjósolják a következő szót egy mondatban, ami elengedhetetlen a beszédfelismerés, a gépi fordítás és az automatikus szövegjavítás területén.
A Zipf-törvény nem csupán egy statisztikai érdekesség, hanem egy gyakorlati eszköz, amely lehetővé teszi a számítógépes nyelvészet és a szövegbányászat számára, hogy hatékonyabban dolgozzanak fel és értelmezzenek nagy mennyiségű szöveges adatot.
A szógyakorisági listák létrehozása és elemzése a Zipf-törvény alapján a szövegbányászat egyik alapvető technikája. Ezek a listák segítenek azonosítani a szöveg korpuszban leggyakrabban előforduló szavakat, és ezáltal a szöveg fő témáit és fogalmait. A ritkább szavak elemzése pedig segíthet a speciálisabb vagy kevésbé nyilvánvaló témák feltárásában.
A Zipf-törvény alkalmazásával a szövegek tömörítése is hatékonyabbá tehető. Mivel a leggyakoribb szavak jelentős részét teszik ki a szövegnek, ezek kódolása rövidebb kódokkal jelentősen csökkentheti a szöveg méretét, miközben a legfontosabb információ megmarad.
A Zipf-törvény szerepe a keresőmotorok működésében és a SEO-ban
A Zipf-törvény, mely egy statisztikai eloszlás leírására szolgál, érdekes összefüggéseket mutat a keresőmotorok működésével és a SEO-val (Search Engine Optimization). Lényege, hogy egy korpuszban (szöveggyűjteményben) a szavak gyakorisága fordítottan arányos a rangsorukkal. Például a leggyakoribb szó körülbelül kétszer olyan gyakori, mint a második leggyakoribb, háromszor olyan gyakori, mint a harmadik, és így tovább.
A keresőmotorok, mint a Google, ezt az elvet figyelembe veszik a tartalom indexelésekor és rangsorolásakor. A gyakori szavak (pl. névelők, kötőszavak) kiszűrése, a ritkább, releváns kulcsszavak azonosítása kulcsfontosságú a keresési eredmények pontosságának növeléséhez. Ezek a gyakori szavak önmagukban kevés információt hordoznak a dokumentum tartalmáról, ezért a keresőmotorok algoritmusaiban általában alacsonyabb súllyal szerepelnek.
A SEO szempontjából a Zipf-törvény azt jelenti, hogy a kulcsszavak kiválasztásánál figyelembe kell venni azok gyakoriságát. Nem elég a leggyakoribb szavakra fókuszálni, mert ezekre nagyon nagy a verseny. Ehelyett érdemes olyan kulcsszavakat találni, amelyek viszonylag gyakoriak, de mégsem túl telítettek a keresőben. Ezt hívják long-tail kulcsszavaknak. Ezek a hosszabb, specifikusabb kifejezések gyakran célzottabb forgalmat generálnak.
A Zipf-törvény rávilágít, hogy a tartalom optimalizálása során nem csak a kulcsszavak puszta jelenléte számít, hanem azok eloszlása és relevanciája is.
Például, ha valaki „cipő” kulcsszóra szeretne optimalizálni, az rendkívül nehéz lenne. Ehelyett érdemes lehet „bőr túracipő férfiaknak” vagy „kényelmes futócipő nőknek” típusú long-tail kulcsszavakat használni.
A kulcsszókutatás során a Zipf-törvény segít megérteni a különböző kifejezések relatív fontosságát és versenyképességét. A keresőmotorok algoritmusa folyamatosan változik, de a statisztikai elvek, mint a Zipf-törvény, alapvető irányelveket adnak a hatékony SEO stratégia kialakításához. A tartalomkészítés során a kulcsszavak természetes, organikus módon történő beépítése, a felhasználói szándék kielégítése, valamint a releváns és értékes tartalom létrehozása mind hozzájárul a jobb helyezés eléréséhez.
A Zipf-törvény és a Pareto-elv (80/20-as szabály) közötti kapcsolat
A Zipf-törvény és a Pareto-elv, más néven a 80/20-as szabály, szorosan összefüggenek. Mindkettő olyan jelenségeket ír le, ahol a legtöbb hatás egy viszonylag kis számú okból vagy elemből származik.
A Pareto-elv azt mondja, hogy körülbelül a hatások 80%-át az okok 20%-a okozza. Például, egy cég bevételének 80%-a az ügyfelek 20%-ától származhat. A Zipf-törvény ehhez hasonlóan azt állítja, hogy egy adott populációban (például egy szövegben) a leggyakoribb szó körülbelül kétszer olyan gyakran fordul elő, mint a második leggyakoribb, háromszor olyan gyakran, mint a harmadik, és így tovább.
Bár a két elv nem azonos, mindkettő azt mutatja, hogy az erőforrások eloszlása nem egyenletes, hanem a kevésbé gyakori elemek sokkal nagyobb arányban vannak jelen, mint a gyakoriak.
Mindkét elv alkalmazható a legkülönbözőbb területeken, a gazdaságtól a nyelvészeten át a szoftverfejlesztésig. A lényeg, hogy felismerjük: nem minden elem egyformán fontos, és a legjelentősebbekre kell összpontosítanunk.
A Zipf-eloszlás egy diszkrét valószínűségi eloszlás, míg a Pareto-eloszlás egy folytonos eloszlás. Ennek ellenére a Pareto-elv gyakran közelíthető a Zipf-törvénnyel diszkrét adathalmazok esetében.
A Zipf-törvény alkalmazása a hálózatkutatásban: Kapcsolatok és csomópontok eloszlása

A hálózatkutatásban a Zipf-törvény figyelemre méltó módon jelenik meg a csomópontok fokszámának eloszlásában. Ez azt jelenti, hogy a hálózatban található csomópontok kapcsolataik száma szerint nem egyenletesen oszlanak el. Épp ellenkezőleg: néhány csomópont (a „hubok”) rengeteg kapcsolattal rendelkezik, míg a legtöbb csomópontnak csak kevés kapcsolata van.
Gondoljunk például a közösségi média hálózatokra. A Zipf-törvény alapján várható, hogy néhány felhasználónak (a befolyásos személyeknek vagy márkáknak) rengeteg követője van, míg a legtöbb felhasználónak csak néhány. Hasonló megfigyelhető az interneten is: néhány weboldal (pl. a Google vagy a Facebook) rengeteg hivatkozást kap, míg a legtöbb weboldalra csak néhány hivatkozás mutat.
A Zipf-törvény a hálózatkutatásban azt sugallja, hogy a hálózatok nem véletlenszerűen épülnek fel, hanem egy hierarchikus struktúrát követnek, ahol néhány csomópont központi szerepet játszik.
Ez a megfigyelés fontos következményekkel jár a hálózatok robosztusságára és sebezhetőségére nézve. Mivel a hálózat működése nagymértékben függ a huboktól, a hubok eltávolítása vagy meghibásodása súlyos következményekkel járhat a hálózat egészére nézve. Ezzel szemben a kevésbé fontos csomópontok eltávolítása kevésbé befolyásolja a hálózat működését.
A Zipf-törvény alkalmazása a hálózatkutatásban lehetővé teszi számunkra, hogy jobban megértsük a hálózatok szerkezetét és működését, valamint hogy előre jelezzük a hálózatok viselkedését különböző körülmények között. A törvény segíthet azonosítani a kritikus csomópontokat, optimalizálni a hálózatok tervezését, és javítani a hálózatok biztonságát.
A Zipf-törvény és a városméretek eloszlása
A Zipf-törvény érdekes módon alkalmazható a városméretek eloszlásának vizsgálatára. A törvény azt állítja, hogy egy adott régióban vagy országban a városok népessége fordítottan arányos a rangsorukkal. Ez azt jelenti, hogy a legnagyobb város népessége nagyjából kétszer akkora, mint a második legnagyobb városé, háromszor akkora, mint a harmadiké, és így tovább.
A Zipf-törvény szerint tehát a városméretek eloszlása nem egyenletes, hanem erősen torzított: kevés nagyváros és sok kisváros található.
Bár a Zipf-törvény nem tökéletes modell, gyakran meglepően jól illeszkedik a valós adatokhoz. Az eltérések oka lehet a történelmi fejlődés, a földrajzi adottságok, vagy a kormányzati politika. Például egy ország fővárosa gyakran jelentősen nagyobb, mint ami a Zipf-törvény alapján várható lenne, mivel a politikai és gazdasági központosítás felerősíti a növekedését.
A törvényt empirikusan vizsgálták számos országban és régióban, és bár az illeszkedés változó, a tendencia általában megfigyelhető. A Zipf-törvény alkalmazása a városméretekre segít megérteni a városfejlődés dinamikáját és a regionális egyenlőtlenségeket.
A Zipf-törvény nemcsak a városméretekre alkalmazható, hanem más jelenségekre is, például a szavak gyakoriságára egy szövegben, vagy a weboldalak látogatottságára az interneten. Ez a széleskörű alkalmazhatóság teszi a Zipf-törvényt egy fontos eszközzé a statisztikai eloszlások elemzésében.
A Zipf-törvény a zeneiparban: Népszerűség és hallgatottság eloszlása
A zeneiparban a Zipf-törvény jól megfigyelhető a népszerűség eloszlásában. Ez azt jelenti, hogy a legnépszerűbb zeneszámok és előadók hallgatottsága nagyságrendekkel magasabb, mint a kevésbé ismerteké. A legnépszerűbb számok uralják a lejátszási listákat és a rádiós adásokat, míg a hatalmas mennyiségű többi zeneszám elenyésző figyelmet kap.
A Zipf-törvény a zeneiparban azt sugallja, hogy a hallgatottság nem egyenletesen oszlik el, hanem a legnépszerűbb tartalmakra koncentrálódik.
Ez a jelenség a digitális zenei platformok működésére is rávilágít. Az algoritmusok, amelyek a felhasználóknak zenét ajánlanak, gyakran a legnépszerűbb tartalmakat részesítik előnyben, tovább erősítve a Zipf-törvény hatását. Ennek következtében a kevésbé ismert előadók és zeneszámok nehezebben jutnak el a közönséghez, ami kihívásokat jelent a feltörekvő művészek számára. A streaming szolgáltatások elterjedésével a hallgatottság még inkább a top előadókra koncentrálódik.
A Zipf-törvény a zeneiparban nem csak a hallgatottságra, hanem a bevételekre is hatással van. A legnépszerűbb zeneszámok generálják a legtöbb bevételt a streaming szolgáltatásokból és a letöltésekből, ami tovább növeli a különbséget a sikeres és a kevésbé sikeres előadók között.
A Zipf-törvény a könyvkiadásban: Eladási adatok és szerzői népszerűség
A Zipf-törvény érdekesen tükröződik a könyvkiadás világában. Az eladási adatok vizsgálatakor feltűnő, hogy a legnépszerűbb könyvek eladási számai sokszorosan felülmúlják a kevésbé népszerűekét. Ez az eloszlás azt mutatja, hogy néhány könyv kiemelkedően sikeres, míg a többi könyv eladási számai fokozatosan csökkennek.
A könyvkiadásban a Zipf-törvény azt jelenti, hogy a könyvek többsége viszonylag kevés példányban kel el, míg néhány cím hatalmas sikert arat.
A szerzői népszerűség is hasonló mintázatot mutat. Néhány szerző neve garancia a sikerre, és könyveik rendszeresen a bestseller listák élén szerepelnek. Ezzel szemben a legtöbb szerző könyvei nem érik el ezt a szintű ismertséget és eladási sikert. Ez a jelenség a „hosszú farok” jelenségként is ismert, ahol sok kisebb eladású termék (jelen esetben könyv) együttesen is jelentős bevételt generálhat, de a néhány kiemelkedő bestseller dominál.
A kiadók ezt a törvényt figyelembe véve alakítják ki stratégiájukat. A bestsellerekbe fektetett marketing erőfeszítések gyakran megtérülnek, míg a kevésbé ismert szerzők támogatása nagyobb kockázatot jelent. A Zipf-törvény a könyvkiadásban tehát nem csupán egy statisztikai megfigyelés, hanem egy fontos szempont a kiadói döntések meghozatalakor.
A Zipf-törvény a tudományos publikációkban: Hivatkozások és impakt faktor

A Zipf-törvény a tudományos publikációk világában is megfigyelhető, különösen a hivatkozások számának eloszlásában. A törvény azt sugallja, hogy kevés publikáció kap rendkívül sok hivatkozást, míg a legtöbb publikáció viszonylag kevés hivatkozást gyűjt.
Ez az eloszlás közvetlen hatással van a tudományos folyóiratok impakt faktorára. Az impakt faktor egy adott folyóiratban megjelent cikkek átlagos hivatkozottságát méri. Mivel a hivatkozások eloszlása nem egyenletes, néhány kiemelkedően hivatkozott cikk jelentősen befolyásolhatja egy folyóirat impakt faktorát.
A Zipf-törvény érvényesülése azt jelenti, hogy az impakt faktor nem feltétlenül tükrözi pontosan a folyóiratban megjelent összes cikk minőségét.
Például, egy folyóirat, amelyben egy-két rendkívül népszerű cikk jelenik meg, magasabb impakt faktorral rendelkezhet, még akkor is, ha a többi cikke kevésbé hivatkozott. Emiatt az impakt faktort kritikával kell kezelni, és más mutatókkal együtt kell figyelembe venni a tudományos munka értékének megítéléséhez.
A tudományos közösség egyre inkább keresi az alternatív metrikákat, amelyek jobban tükrözik a tudományos publikációk valós hatását és értékét, elkerülve a Zipf-törvény által okozott torzításokat. Ilyen metrikák például az Altmetrics, melyek a közösségi média figyelmét, a hírekben való megjelenést és a tudományos blogokban való említéseket is figyelembe veszik.
A Zipf-törvény korlátai és kritikái: Mikor nem alkalmazható a törvény?
Bár a Zipf-törvény számos területen megfigyelhető, nem univerzális érvényű. Alkalmazhatósága korlátozott, és fontos tisztában lenni azokkal a helyzetekkel, amikor nem ad pontos képet a valóságról.
Először is, a törvény nem alkalmazható kis adathalmazokra. Ahhoz, hogy a Zipf-eloszlás érvényesüljön, elegendő mennyiségű adat szükséges. Kis minták esetén a véletlen ingadozások torzíthatják az eredményeket.
Másodszor, a Zipf-törvény nem feltételezi a szavak jelentését vagy a kontextust. Egyszerűen csak a szavak gyakoriságát vizsgálja. Ez azt jelenti, hogy a törvény nem tud különbséget tenni a különböző jelentésű, de azonos gyakoriságú szavak között.
A Zipf-törvény nem magyarázza meg a szavak jelentésének vagy a szövegkörnyezetnek a szerepét a nyelvi jelenségekben.
Harmadszor, bizonyos nyelvek vagy szövegtípusok eltérést mutathatnak a Zipf-eloszlástól. Például, a szigorúan szerkesztett szakmai szövegekben vagy a formális nyelvi stílusban a szavak eloszlása kevésbé tükrözi a Zipf-törvényt, mint a spontán beszédben.
Végül, a Zipf-törvény nem ad magyarázatot a jelenség okaira, csupán leírja a statisztikai eloszlást. Nem tudjuk meg belőle, hogy *miért* pont így alakul a szavak gyakorisága, csak azt, hogy *hogyan*.
Alternatív statisztikai eloszlások: Power law, log-normális eloszlás és más modellek
A Zipf-törvény egy speciális esete a power law eloszlásnak. A power law eloszlások lényege, hogy a gyakoriság fordítottan arányos a rangsorral, azaz a leggyakoribb elem sokkal gyakoribb, mint a kevésbé gyakoriak. Bár a Zipf-törvény jól leír bizonyos jelenségeket, gyakran találkozunk olyan adatokkal, amelyekre más eloszlások illeszkednek jobban.
A log-normális eloszlás egy másik gyakran használt modell, különösen akkor, ha az adatok szorzati folyamatok eredményeként jönnek létre. Például, ha egy szó gyakorisága több tényező szorzataként alakul ki (pl. a szerző stílusa, a téma relevanciája, a célközönség), akkor a log-normális eloszlás jobb illeszkedést mutathat, mint a Zipf-törvény.
Egyéb modellek is léteznek, amelyek alkalmasak lehetnek a statisztikai eloszlások leírására. Ilyenek például az exponenciális eloszlás, a Weibull-eloszlás és a Pareto-eloszlás (amely szintén egyfajta power law eloszlás). A megfelelő modell kiválasztása az adatok jellegétől és a vizsgált jelenség mögötti mechanizmusoktól függ.
A valóságban ritka, hogy egyetlen eloszlás tökéletesen leírjon egy adott jelenséget. Gyakran a legjobb megoldás a különböző modellek kombinációja, vagy egy olyan modell, amely figyelembe veszi a jelenség összetettségét.
Például, a kevert eloszlások lehetővé teszik, hogy különböző populációkhoz különböző eloszlásokat rendeljünk. Ez hasznos lehet például a nyelvi adatok elemzésénél, ahol a különböző szövegtípusok (pl. szépirodalom, tudományos szövegek) eltérő statisztikai jellemzőkkel rendelkeznek.
A megfelelő statisztikai modell kiválasztása kulcsfontosságú a pontos elemzéshez és a megbízható következtetések levonásához. A Zipf-törvény egy hasznos kiindulópont, de a valós adatok gyakran összetettebbek, és más modellek alkalmazását teszik szükségessé.
A Zipf-törvény illeszkedésének tesztelése és a mérőszámok értelmezése
A Zipf-törvény illeszkedését különböző statisztikai mérőszámokkal tesztelhetjük. Az egyik leggyakoribb módszer a Pearson-féle korrelációs együttható számítása, mely a rangsor és a gyakoriság közötti kapcsolatot méri. Magas korreláció (közel -1) erős negatív kapcsolatot jelez, ami alátámasztja a törvényt.
Egy másik fontos mérőszám a Kolmogorov-Smirnov teszt, amely a mért adatok eloszlását hasonlítja össze az ideális Zipf-eloszlással. A teszt eredménye egy p-érték, mely ha alacsonyabb egy előre meghatározott szignifikancia szintnél (pl. 0.05), akkor elutasíthatjuk azt a hipotézist, hogy az adatok Zipf-eloszlást követnek.
A mérőszámok értelmezésekor figyelembe kell venni, hogy a Zipf-törvény közelítő jelenség, és ritkán teljesül tökéletesen a valós adatokban.
A mérőszámok önmagukban nem elegendőek. Érdemes vizuálisan is ellenőrizni az illeszkedést, például rang-gyakoriság diagramot készítve. A diagramon a rangsorolt elemek gyakoriságát ábrázoljuk, és ha az adatok Zipf-eloszlást követnek, a diagram egy közel lineáris csökkenést mutat log-log skálán.
Az illeszkedés jóságának megítéléséhez a paraméterbecslés is hozzájárul. A Zipf-törvény egyetlen paramétert, az exponens értékét tartalmazza. A becsült exponens értékének összehasonlítása a várt értékkel (általában 1 közelében) további információt nyújt az illeszkedés minőségéről.
A Zipf-törvény generálása szimulációk segítségével
A Zipf-törvény, mely a gyakoriság és a rang közötti kapcsolatot írja le, szimulációk segítségével is generálható. Ezek a szimulációk gyakran egyszerű véletlenszerű folyamatokon alapulnak, amelyek meglepő módon képesek a törvényt reprodukálni.
Egy népszerű megközelítés a preferenciális kapcsolódás elve. Ebben a modellben az új elemek nagyobb valószínűséggel kapcsolódnak a már népszerű elemekhez. Képzeljünk el egy szótárat, ahol az új szavak nagyobb eséllyel kerülnek felhasználásra a már gyakran használt szavak környezetében. Ez a folyamat önmagában is képes egy Zipf-eloszláshoz hasonló eloszlást létrehozni.
Más szimulációk véletlenszerű növekedési folyamatokat használnak. Például, egy egyszerű modellben minden szó egyenlő eséllyel indul, majd véletlenszerűen kerül kiválasztásra. Minden kiválasztás növeli a szó gyakoriságát. Hosszú távon, a véletlen ingadozások miatt néhány szó gyakorisága sokkal magasabb lesz, mint másoké, létrehozva egy Zipf-eloszlást.
A szimulációk azt mutatják, hogy a Zipf-törvény nem feltétlenül igényel bonyolult magyarázatokat; egyszerű, véletlenszerű folyamatok is képesek a jelenséget reprodukálni.
A szimulációk segítségével kísérletezhetünk különböző paraméterekkel, és megvizsgálhatjuk, hogyan befolyásolják a végső eloszlást. Például, a preferenciális kapcsolódás erősségének változtatásával megfigyelhetjük, hogyan változik a Zipf-eloszlás meredeksége. Ezek a kísérletek segítenek jobban megérteni a Zipf-törvény mögött rejlő mechanizmusokat.
Fontos megjegyezni, hogy a szimulációk nem tökéletes másolatai a valós világnak, de hasznos eszközök a Zipf-törvény alapvető elveinek feltárásához.
A Zipf-törvény alkalmazása az adatkompresszióban
A Zipf-törvény, mely szerint a leggyakoribb elem előfordulási gyakorisága a legritkább elem előfordulási gyakoriságának többszöröse, kulcsszerepet játszik az adatkompressziós algoritmusokban. Az elv az, hogy kihasználjuk az adatok egyenlőtlen eloszlását a hatékonyabb tárolás érdekében.
Az adatkompresszió során a leggyakoribb szimbólumokhoz (pl. betűk, szavak, bitek) rövidebb kódokat rendelünk, míg a ritkábbakhoz hosszabbakat. Ennek eredményeként a teljes adatmennyiség csökken, mivel a gyakori elemek kevesebb bittel kerülnek reprezentálásra.
A Zipf-törvény lehetővé teszi, hogy előrejelezzük a különböző adatok gyakoriságát, és ezáltal optimalizáljuk a kompressziós algoritmusokat.
Például a Huffman-kódolás és az aritmetikai kódolás is a Zipf-törvényen alapuló eljárások. Ezek az algoritmusok elemzik az adatokat, meghatározzák a szimbólumok gyakoriságát, majd ennek megfelelően állítják be a kódokat. Minél jobban igazodik az adathalmaz a Zipf-törvényhez, annál hatékonyabb a kompresszió.
Az elmélet alkalmazásával jelentősen csökkenthető a tárolási helyigény és a sávszélesség, ami különösen fontos a nagy mennyiségű adatot kezelő rendszereknél. A minél pontosabb gyakorisági elemzés elengedhetetlen a hatékony adatkompresszióhoz.
A Zipf-törvény modellezése különböző programozási nyelveken (pl. Python, R)
A Zipf-törvény modellezése különböző programozási nyelveken, mint például a Python és az R, lehetővé teszi számunkra, hogy vizualizáljuk és elemezzük ezt a gyakran előforduló statisztikai eloszlást. A törvény lényege, hogy egy populációban a rangsor és a gyakoriság között fordított arányosság áll fenn. Például, egy szövegkorpuszban a leggyakoribb szó kétszer olyan gyakran fordul elő, mint a második leggyakoribb, háromszor olyan gyakran, mint a harmadik, és így tovább.
Pythonban a matplotlib könyvtár segítségével könnyen ábrázolhatjuk a Zipf-eloszlást. Először beolvassuk az adatokat (például szavak gyakoriságát egy szövegfájlból), majd kiszámítjuk a szavak rangsorát. Ezt követően egy szórásdiagramon (scatter plot) ábrázoljuk a rangsort a gyakoriság függvényében. A kapott grafikonon egy jellegzetes, lefelé ívelő görbe látható, amely szemlélteti a Zipf-törvényt.
R-ben a ggplot2 csomag kínál hasonló vizualizációs lehetőségeket. Az adatok előkészítése után a ggplot() függvény segítségével hozhatunk létre diagramokat. Az geom_point() függvény alkalmas a szórásdiagram ábrázolására, míg a scale_x_log10() és scale_y_log10() függvényekkel logaritmikus skálázást alkalmazhatunk a tengelyeken, ami segít jobban láthatóvá tenni a törvényt.
A Zipf-törvény modellezése segít megérteni a természetes nyelvi adatok szerkezetét, a weboldalak látogatottságát, a városok népességét és számos más jelenséget.
Mindkét nyelvben fontos, hogy az adatok megfelelően legyenek előkészítve. Ez magában foglalja a szövegtisztítást (például a központozás eltávolítását), a szavak megszámolását és a gyakoriságok kiszámítását. Ezen felül, érdemes megvizsgálni, hogy az adatok mennyire követik pontosan a Zipf-törvényt, és az esetleges eltéréseket elemezni.
A modellezés során figyelembe kell venni, hogy a Zipf-törvény egy empirikus megfigyelés, nem pedig egy szigorú matematikai törvény. Ez azt jelenti, hogy a valós adatokban gyakran találhatók eltérések a tökéletes Zipf-eloszlástól. Ezek az eltérések értékes információkat hordozhatnak az adatok eredetéről és a generáló folyamatokról.
A Zipf-törvény vizualizációja: Grafikonok és ábrák készítése
A Zipf-törvény vizuális megjelenítése kulcsfontosságú a jelenség megértéséhez. Gyakran használunk log-log grafikonokat, ahol mindkét tengelyen logaritmikus skála szerepel. Ezen a grafikonon a Zipf-törvény egy közelítőleg egyenes vonalként jelenik meg, melynek meredeksége jellemzően -1 körül van. Ez azt jelenti, hogy a rangsor és a gyakoriság között fordított, hatványkitevős kapcsolat áll fenn.
A grafikonok segítségével könnyen összehasonlíthatók különböző adathalmazok, például különböző nyelvek szógyakorisági eloszlásai. Az eltérések a meredekségben és az eltolásban árulkodóak lehetnek a szövegek jellegéről vagy a nyelvek sajátosságairól.
A Zipf-törvény vizualizációja lehetővé teszi, hogy az adatok mögött rejlő mintázatokat intuitív módon megragadjuk.
A vizualizáció során gyakran használunk szófelhőket is, ahol a szavak mérete a gyakoriságukkal arányos. Ez a módszer különösen alkalmas arra, hogy egy szöveg legfontosabb elemeit gyorsan azonosítsuk.
A vizuális ábrázolás kiterjedhet a kumulatív gyakoriságok ábrázolására is, amely megmutatja, hogy a leggyakoribb szavak az összes szó hány százalékát teszik ki. Ez segíthet megérteni, hogy milyen mértékben koncentrálódik a gyakoriság a leggyakoribb elemekre.
A Zipf-törvény és a long tail jelenség közötti összefüggés
A Zipf-törvény egy empirikus megfigyelés, amely számos területen megmutatkozik, beleértve a nyelvet, a populációt és az internetes forgalmat. A törvény lényege, hogy egy populációban a leggyakoribb elem gyakorisága körülbelül kétszerese a második leggyakoribb elem gyakoriságának, háromszorosa a harmadikénak, és így tovább. Ez az eloszlás jellemzően a „long tail” jelenséghez vezet.
A „long tail” (hosszú farok) azt jelenti, hogy a populáció nagy része kis számú, nagyon népszerű elemre koncentrálódik, míg a fennmaradó, kevésbé népszerű elemek hosszú „farkat” alkotnak. Például, a könyvek eladásában kevés a bestseller, ami magas példányszámban kel el, míg sok más könyv eladása alacsony, de együttesen jelentős bevételt generálhatnak.
A Zipf-törvény és a long tail jelenség szorosan összefüggenek: a Zipf-törvény egy matematikai modell, amely leírja a long tail eloszlását.
Az internet térhódításával a long tail jelenség még inkább felerősödött. A digitális platformok (pl. online áruházak, videómegosztó oldalak) lehetővé teszik, hogy a felhasználók hozzáférjenek a korábban nehezen elérhető, kevésbé népszerű termékekhez és tartalmakhoz. Ezáltal a long tail elemek összességében jelentős piaci részesedést szerezhetnek.
A marketing és az üzleti stratégia szempontjából a long tail jelenség fontos következményekkel jár. A vállalatoknak nem csak a népszerű termékekre kell koncentrálniuk, hanem érdemes figyelmet fordítaniuk a kevésbé népszerű, de együttesen jelentős bevételt hozó termékekre is. A long tail stratégiák lehetővé teszik a vállalatok számára, hogy speciális igényeket elégítsenek ki, és új piaci szegmenseket hódítsanak meg.
A Zipf-törvény alkalmazása a közösségi médiában: Tartalmak terjedése és népszerűsége
A Zipf-törvény a közösségi médiában is megfigyelhető, különösen a tartalmak terjedése és népszerűsége tekintetében. A törvény lényege, hogy a leggyakoribb elem (például a legnépszerűbb poszt) sokkal gyakrabban fordul elő, mint a második leggyakoribb, és így tovább, egy erősen csökkenő görbét mutatva. Ez azt jelenti, hogy a legnépszerűbb tartalmak rendkívül nagy figyelmet kapnak, míg a kevésbé népszerűek szinte teljesen eltűnnek a zajban.
A közösségi médiában ez abban nyilvánul meg, hogy a legnézettebb videók, a legtöbb lájkot kapott posztok és a leggyakrabban megosztott cikkek kiemelkedően teljesítenek a többi tartalomhoz képest. Ezt a jelenséget a hálózati hatás erősíti, ahol a már népszerű tartalom még népszerűbbé válik, mivel az emberek nagyobb valószínűséggel osztják meg vagy nézik meg azt, amit már sokan mások is tettek.
A Zipf-törvény a közösségi médiában azt jelenti, hogy a tartalomgyártók törekvései ellenére csak néhány tartalom válik igazán virálissá, míg a többség a háttérben marad.
A marketing szakemberek és tartalomgyártók számára a Zipf-törvény megértése kulcsfontosságú. Felismerhetik, hogy a népszerűség eloszlása nem egyenletes, és a befektetett erőfeszítések nem feltétlenül eredményeznek egyenletes sikert. Ehelyett a hangsúlyt a potenciálisan virálissá váló tartalmak létrehozására és a már népszerű tartalmak kihasználására kell helyezni.
Például, ha egy márka észreveszi, hogy egy bizonyos típusú poszt (pl. egy vicces mém vagy egy érzelmes történet) nagy népszerűségnek örvend, akkor érdemes hasonló tartalmakat gyártani és terjeszteni. Fontos azonban megjegyezni, hogy a közösségi média algoritmusai is befolyásolják a tartalmak terjedését, így a Zipf-törvény nem az egyetlen tényező, ami a népszerűséget meghatározza.