A szabadságfok (degrees of freedom, DOF) egy mechanikai rendszer állapotának leírásához szükséges független paraméterek minimális számát jelöli. Egyszerűbben fogalmazva, megmutatja, hogy egy objektum vagy rendszer hányféleképpen mozoghat.
Például, egy síkon mozgó pontnak két szabadságfoka van: az x és y koordinátái. Egy térben mozgó pontnak pedig három: x, y és z. Minél összetettebb a rendszer, annál több szabadságfoka lehet. Egy merev testnek a térben hat szabadságfoka van: három eltolási (x, y, z) és három forgási (a három tengely körül).
A szabadságfokok ismerete kulcsfontosságú a mechanikai rendszerek viselkedésének előrejelzéséhez és modellezéséhez.
A szabadságfok fogalma nem korlátozódik kizárólag a mechanikára. Megjelenik a statisztikában, a termodinamikában és más tudományterületeken is, ahol a rendszer leírásához szükséges független változók számát jelenti.
A robotikában például a robotkar szabadságfokainak száma meghatározza, hogy milyen komplex mozgásokat képes végrehajtani. Minél több szabadságfoka van, annál rugalmasabban és precízebben tud mozogni. Ugyanakkor a több szabadságfok bonyolultabb vezérlést is igényel.
A szabadságfok definíciója és alapelvei
A szabadságfok egy mechanikai rendszer független koordinátáinak számát jelöli, amelyek szükségesek a rendszer konfigurációjának teljes leírásához. Egyszerűbben fogalmazva, megmutatja, hogy hányféleképpen mozoghat egy objektum vagy rendszer a térben.
A szabadságfok fogalma kulcsfontosságú a mechanika, a robotika és a mérnöki tudományok számos területén. Segítségével modellezhetjük és elemezhetjük a mozgást, tervezhetünk gépeket és robotokat, valamint szimulálhatunk fizikai rendszereket.
A szabadságfok azt mutatja meg, hogy egy test, vagy rendszer hány egymástól független irányban képes mozogni.
Egy pontszerű testnek a térben három szabadságfoka van: elmozdulhat az x, y és z tengelyek mentén. Egy merev testnek emellett három forgási szabadságfoka is van, azaz foroghat az x, y és z tengelyek körül. Így egy merev testnek a térben összesen hat szabadságfoka van.
A szabadságfokok számát befolyásolhatják a kényszerek. A kényszerek korlátozzák a rendszer mozgását. Például, ha egy test egy sík felületen mozog, akkor csak két elmozdulási szabadságfoka van (x és y), mivel nem tud elmozdulni a z tengely mentén. Ha egy test egy rúdhoz van rögzítve, akkor a rúd hossza korlátozza a mozgását, és csökkenti a szabadságfokok számát.
Néhány példa a szabadságfokokra:
- Egy autó: A legtöbb autó rendelkezik 3 szabadságfokkal (előre/hátra, jobbra/balra, és a függőleges tengely körüli elfordulás).
- Egy ajtó: Egy tipikus ajtónak egyetlen szabadságfoka van (a zsanérok mentén való forgás).
- Egy emberi kar: Az emberi karnak több szabadságfoka van, mivel a váll, a könyök és a csukló is lehetővé teszik a mozgást.
A szabadságfokok számának meghatározása segít a mérnököknek megérteni és irányítani a gépek és robotok mozgását. Például, egy robotkar tervezésénél figyelembe kell venni a szükséges szabadságfokokat ahhoz, hogy a robot el tudja végezni a kívánt feladatot.
A szabadságfokok számának pontos ismerete elengedhetetlen a mechanikai rendszerek helyes modellezéséhez és szimulációjához. A túl kevés szabadságfok pontatlan eredményekhez vezethet, míg a túl sok szabadságfok feleslegesen bonyolulttá teheti a modellt.
A merev test szabadságfokai: transzlációs és rotációs mozgások
A szabadságfok egy mechanikai rendszer azon független paramétereinek száma, amelyek szükségesek a rendszer konfigurációjának teljes leírásához. Egyszerűbben fogalmazva, megmutatja, hányféleképpen mozoghat egy test a térben.
A merev testek esetében, amelyek nem deformálódnak, a szabadságfokokat a transzlációs és rotációs mozgások kombinációja adja. A transzlációs mozgás a test helyének megváltozását jelenti, míg a rotációs mozgás a test elfordulását egy tengely körül.
Egy merev testnek a háromdimenziós térben összesen hat szabadságfoka van: három transzlációs és három rotációs.
A transzlációs szabadságfokok a három koordináta-tengely (x, y, z) mentén történő elmozdulásokat írják le. Képzeljünk el egy kockát. Ezt a kockát elmozdíthatjuk jobbra-balra (x tengely), előre-hátra (y tengely), illetve fel-le (z tengely). Mindegyik tengely mentén történő elmozdulás egy-egy szabadságfokot jelent.
A rotációs szabadságfokok a három koordináta-tengely (x, y, z) körüli elfordulásokat írják le. Ugyanezt a kockát elforgathatjuk az x, y és z tengelyek körül. Minden tengely körüli elfordulás egy-egy rotációs szabadságfokot jelent.
Például, egy repülőgépnek hat szabadságfoka van: három transzlációs (előre/hátra, oldalra, fel/le) és három rotációs (bólogatás, dőlés, perdülés). Ezek a szabadságfokok határozzák meg a gép mozgását a térben.
A szabadságfokok fogalma kritikus a mechanikai rendszerek modellezésében és szimulációjában. A szabadságfokok ismerete elengedhetetlen ahhoz, hogy megértsük és előrejelezzük egy rendszer viselkedését, például egy robotkar mozgását vagy egy jármű dinamikáját.
A szabadságfokok korlátozása befolyásolja a rendszer mozgását. Például, egy sínen mozgó vonatnak kevesebb szabadságfoka van, mint egy szabadon mozgó autónak, mivel a vonat mozgása a sínre van korlátozva.
Pontszerű test szabadságfokai

A szabadságfok egy mechanikai rendszer azon független paramétereinek száma, amelyek szükségesek a rendszer konfigurációjának teljes leírásához. Egyszerűbben fogalmazva, megmutatja, hányféleképpen mozoghat egy test.
Egy pontszerű test, melynek mérete és belső szerkezete elhanyagolható, a térben három szabadságfokkal rendelkezik. Ez azt jelenti, hogy a térben három egymástól független irányban mozgatható: a háromdimenziós térben (x, y és z tengelyek mentén).
Tehát egy pontszerű test helyzetét a térben három koordináta egyértelműen meghatározza, és mindhárom koordináta függetlenül változhat.
Például, ha egy pontszerű test egy síkon mozog, akkor csak két szabadságfoka van, mivel csak két koordináta (x és y) szükséges a helyzetének leírásához. Ha a test egy egyenes mentén kényszerül mozogni, akkor pedig csak egy szabadságfoka van.
A szabadságfokok számának ismerete elengedhetetlen a mechanikai rendszerek viselkedésének elemzéséhez és modellezéséhez.
Kényszerek és a szabadságfokok csökkentése
A szabadságfokok (DOF) számát a mechanikai rendszerek mozgását korlátozó kényszerek jelentősen befolyásolják. Minél több kényszer hat egy rendszerre, annál kevesebb szabadságfoka marad.
A kényszerek a rendszer lehetséges mozgásait szűkítik le. Például, egy asztalon fekvő tárgy mozgását a gravitáció és az asztal felülete korlátozza. Függőlegesen nem mozoghat, csak vízszintesen, és az asztalon belül. Ez a korlátozás csökkenti a szabadságfokainak számát.
A kényszerek a rendszer mozgását meghatározott pályákra vagy konfigurációkra kényszerítik, ezáltal csökkentve a független változók számát, amelyekkel a rendszer állapotát le lehet írni.
Nézzünk néhány példát:
- Csuklópont: Egy csuklópont két testet köt össze, de lehetővé teszi a forgást. Ez a kötés csökkenti a lineáris mozgások számát, de a forgást megtartja.
- Fix rögzítés: A fix rögzítés minden mozgást megakadályoz, mind a lineárisat, mind a forgásit. Ez a legtöbb szabadságfokot elveszi.
- Sínen mozgó kocsi: A kocsi csak a sín mentén mozoghat, így a többi irányú mozgás korlátozott.
A kényszerek hatása különösen fontos a robotikában és a mechanikai tervezésben. A robotok mozgását úgy tervezik meg, hogy a megfelelő számú szabadságfokkal rendelkezzenek a feladatuk elvégzéséhez. A kényszerek helyes alkalmazása lehetővé teszi a pontos és hatékony mozgást.
A kényszerek típusai sokfélék lehetnek. Lehetnek geometriai kényszerek, amelyek a rendszer alakjából adódnak, vagy kinematikai kényszerek, amelyek a mozgásokat korlátozzák. A kényszerek megértése és helyes modellezése kulcsfontosságú a mechanikai rendszerek viselkedésének pontos előrejelzéséhez.
Holonom és nem-holonom kényszerek
A szabadságfokok számának meghatározásakor fontos figyelembe venni a rendszerre ható kényszereket. Ezek a kényszerek korlátozzák a rendszer mozgását, ezáltal csökkentik a szabadságfokok számát. A kényszereket két fő csoportba sorolhatjuk: holonom és nem-holonom kényszerek.
A holonom kényszerek olyan kényszerek, amelyek kifejezhetők a rendszer koordinátáinak és esetleg az időnek a függvényében. Ezek a kényszerek egy egyenlettel leírhatók, ami közvetlenül összekapcsolja a koordinátákat. Egy egyszerű példa erre egy inga esete, ahol a kötél hossza állandó. Ekkor a lengő test pozícióját korlátozza ez a kötélhosszúság, ami egy holonom kényszert jelent. A holonom kényszerek csökkentik a rendszer szabadságfokainak számát, mivel a koordináták nem függetlenek egymástól.
Ezzel szemben a nem-holonom kényszerek nem fejezhetők ki ilyen egyszerű egyenletekkel. Általában a sebességekre vagy a mozgás irányára vonatkoznak. Egy tipikus példa a guruló kerék esete. A kerék mozgása korlátozott, mivel nem csúszhat oldalra. Ez a kényszer, bár korlátozza a mozgást, nem fejezhető ki egy egyszerű egyenlettel a kerék pozíciójára vonatkozóan. A nem-holonom kényszerek bonyolultabbak, mint a holonom kényszerek, és a rendszer dinamikájának elemzésekor külön figyelmet igényelnek.
A különbség a holonom és nem-holonom kényszerek között abban rejlik, hogy a holonom kényszerek integrálhatók, míg a nem-holonom kényszerek nem.
A nem-holonom kényszerek gyakran előfordulnak a robotikában és az irányítástechnikában, ahol a rendszerek mozgását precízen kell szabályozni. A nem-holonom robotok, például az autók, képesek bizonyos irányokba mozogni, de nem képesek oldalirányú mozgásra. Ez a korlátozás a nem-holonom kényszer következménye.
Az alábbi táblázat összefoglalja a két kényszertípus közötti főbb különbségeket:
| Jellemző | Holonom kényszer | Nem-holonom kényszer |
|---|---|---|
| Kifejezhetőség | Egyenlettel leírható (koordináták függvénye) | Nem fejezhető ki egyenlettel (sebesség/irány függvénye) |
| Integrálhatóság | Integrálható | Nem integrálható |
| Hatás a szabadságfokra | Csökkenti a szabadságfokok számát | Korlátozza a mozgást, de nem feltétlenül csökkenti a szabadságfokok számát ugyanúgy, mint a holonom kényszerek. |
| Példa | Inga kötélhossza | Guruló kerék nem csúszhat oldalra |
A szabadságfok matematikai leírása: koordináták és konfigurációs tér
A szabadságfok fogalma a mechanikában egy rendszer mozgásának leírásához szükséges független koordináták számát jelenti. Ahhoz, hogy a rendszer állapotát teljesen meghatározzuk egy adott pillanatban, ennyi paraméter értékét kell ismernünk. Ezek a koordináták lehetnek lineáris elmozdulások, szögelfordulások, vagy ezek kombinációi.
Matematikailag a szabadságfok a rendszer konfigurációs terének dimenziójával egyezik meg. A konfigurációs tér az összes lehetséges pozíció és orientáció halmaza, amit a rendszer felvehet. Például egy pont a síkon két szabadságfokkal rendelkezik (x és y koordináták), míg a térben hárommal (x, y és z koordináták).
Egy merev test a térben hat szabadságfokkal rendelkezik: három transzlációs (elmozdulás az x, y és z tengelyek mentén) és három rotációs (elfordulás a tengelyek körül). Ezek a független mozgások teszik lehetővé, hogy a test bármilyen pozíciót és orientációt felvegyen a térben.
A szabadságfokok számát befolyásolhatják kényszerek. A kényszer olyan korlátozás, amely csökkenti a rendszer mozgási lehetőségeit. Például, ha egy pont egy adott görbére van kényszerítve, akkor a szabadságfokainak száma lecsökken egyre, mivel a pozícióját egyetlen paraméterrel (a görbén való elhelyezkedésével) leírhatjuk.
A konfigurációs tér tehát nem más, mint az a matematikai tér, amely a rendszer összes lehetséges állapotát tartalmazza, és a szabadságfokok száma ennek a térnek a dimenziója.
A szabadságfokok meghatározása kulcsfontosságú a mechanikai rendszerek modellezésében és szimulációjában. A megfelelő koordináták kiválasztása és a kényszerek figyelembe vétele lehetővé teszi, hogy pontosan leírjuk a rendszer viselkedését és előre jelezzük a mozgását.
A koordináták kiválasztása nem egyértelmű, de célszerű olyan koordinátákat választani, amelyek függetlenek és minimalizálják a kényszerek kezelésével járó bonyodalmakat. Például robotkarok esetében a csuklók szögei gyakran jó választásnak bizonyulnak.
Példák:
- Egy inga: 1 szabadságfok (a kitérés szöge).
- Egy autó: 3 szabadságfok (2D-ben: x, y pozíció és a forgási szög).
- Egy robotkar: a csuklók számától függően több szabadságfok.
A matematikai leírás során fontos, hogy tisztában legyünk a rendszer geometriájával és a rá ható kényszerekkel. A konfigurációs tér pontos meghatározása elengedhetetlen a rendszer dinamikájának és kinematikájának helyes leírásához.
Koordináták típusai: Descartes, polár, hengeres és gömbi koordináták
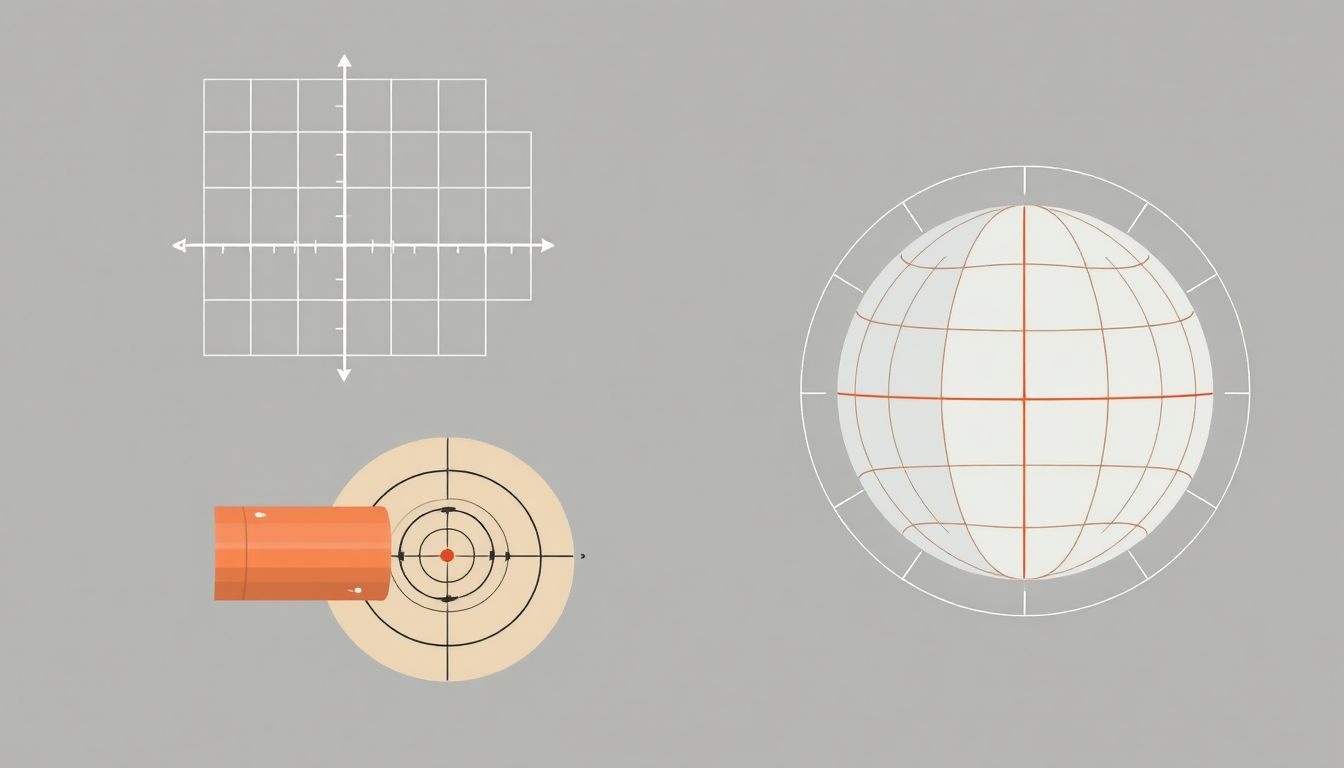
A szabadságfok fogalma a mechanikában szorosan összefügg azzal, hogy egy objektumot milyen koordináta-rendszerben írunk le. Minél több szabadságfoka van egy testnek, annál több független koordinátára van szükség a pozíciójának és orientációjának egyértelmű meghatározásához.
A Descartes-koordináták a leggyakrabban használtak. Két dimenzióban (2D) két szabadságfok szükséges (x, y), míg három dimenzióban (3D) három (x, y, z). Ezek a koordináták lineáris elmozdulásokat írnak le a tengelyek mentén.
A polárkoordináták (r, θ) egy pont helyzetét a középponttól mért távolsággal (r) és a vízszintes tengellyel bezárt szöggel (θ) adják meg. 2D-ben a szabadságfok továbbra is kettő, de a leírás módja eltér a Descartes-koordinátáktól. Ez a leírás gyakran hasznos forgó mozgások vagy körkörös pályák esetén.
A hengeres koordináták a polárkoordináták 3D-s kiterjesztése (r, θ, z). Az ‘r’ és ‘θ’ a vízszintes síkon definiálják a pont helyzetét, míg a ‘z’ a magasságot jelöli. Ebben az esetben a szabadságfok három. A hengeres koordináták különösen hasznosak tengelyszimmetriával rendelkező problémák esetén.
A gömbi koordináták (ρ, θ, φ) egy pontot a középponttól mért távolsággal (ρ), a horizontális síkkal bezárt szöggel (φ, azaz a zenitszöggel) és a horizontális síkban mért szöggel (θ, azaz az azimutszöggel) határoznak meg. Itt is három szabadságfok van. Gömbi koordináták előnyösek olyan helyzetekben, ahol gömbszimmetria áll fenn, például a gravitációs erőtér leírásakor.
A koordináta-rendszer megválasztása nagyban befolyásolhatja a mechanikai problémák megoldásának egyszerűségét.
Például, egy merev testnek 3D-ben 6 szabadságfoka van: 3 a transzlációra (elmozdulásra) és 3 a rotációra (elfordulásra). A forgási szabadságfokokat Euler-szögekkel vagy kvaterniókkal is leírhatjuk, attól függően, hogy milyen szempontból előnyösebb a mozgás leírása.
A konfigurációs tér fogalma és jelentősége
A konfigurációs tér egy absztrakt matematikai tér, amely teljesen leírja egy mechanikai rendszer állapotát. Ez a tér nem a valós tér, amiben élünk, hanem egy olyan tér, ahol minden koordináta egy-egy szabadságfoknak felel meg. Tehát, ha egy rendszernek három szabadságfoka van, akkor a konfigurációs tere egy háromdimenziós tér lesz.
Például, egy merev test a térben hat szabadságfokkal rendelkezik: három a helyzetének (x, y, z) és három a tájolásának (például Euler-szögek) meghatározásához. Ennek a merev testnek a konfigurációs tere tehát egy hatdimenziós tér lenne. Minden pont ebben a hatdimenziós térben a test egy lehetséges helyzetét és tájolását reprezentálja.
A konfigurációs tér azért hasznos, mert lehetővé teszi a rendszer összes lehetséges állapotának áttekintését. Ahelyett, hogy a rendszer mozgását a valós térben vizsgálnánk, a konfigurációs térben egyetlen pont mozgásaként ábrázolhatjuk.
A konfigurációs tér különösen fontos a robotikában, ahol a robot karjának összes lehetséges pozícióját és orientációját kell meghatározni, figyelembe véve a csuklók korlátait.
A konfigurációs térben az akadályok, amelyek a robot mozgását korlátozzák, szintén megjeleníthetők. Ez lehetővé teszi, hogy olyan útvonaltervező algoritmusokat alkalmazzunk, amelyek a robotot biztonságosan, az akadályokat elkerülve vezetik végig a célhelyzetéig. A konfigurációs térben egy „út” a robot karjának egy olyan sorozata, amely során a robot folyamatosan mozog, és soha nem ütközik akadályba.
A konfigurációs tér fogalma nem korlátozódik a mechanikai rendszerekre. Használható más rendszerek leírására is, ahol a rendszer állapotát valamilyen paraméterek halmaza határozza meg. Például a konfigurációs tér felhasználható egy kémiai reakció leírására, ahol a koordináták az atomok közötti távolságok lehetnek.
A szabadságfok meghatározása különböző mechanikai rendszerekben: példák
A szabadságfok egy mechanikai rendszerben azt mutatja meg, hogy hány független paraméter szükséges a rendszer helyzetének egyértelmű leírásához. Más szóval, megmutatja, hányféleképpen mozoghat a rendszer.
Például, egy síkon mozgó pontnak két szabadságfoka van: elmozdulhat az x és az y tengely mentén. Egy térben mozgó pontnak pedig három szabadságfoka van: elmozdulhat az x, y és z tengelyek mentén.
Merev testek esetében a helyzet bonyolultabb. Egy síkon mozgó merev testnek három szabadságfoka van: elmozdulhat az x és y tengely mentén, valamint elforoghat a síkban. Egy térben mozgó merev testnek pedig hat szabadságfoka van: elmozdulhat az x, y és z tengelyek mentén, valamint elforoghat mindhárom tengely körül.
A szabadságfokok számát befolyásolhatják a kényszerek. Például, ha egy pontnak egy vonalon kell mozognia, akkor csak egy szabadságfoka van. Ha egy merev test rögzítve van egy pontban, akkor csak forogni tud, így a szabadságfokainak száma csökken.
A szabadságfokok számának meghatározása elengedhetetlen a mechanikai rendszerek viselkedésének megértéséhez és modellezéséhez.
Nézzünk néhány konkrét példát:
- Inga: Egy egyszerű, kétdimenziós ingának egy szabadságfoka van, a lengési szöge.
- Kerékpáros: Egy kerékpárosnak több szabadságfoka is van, beleértve az előrehaladást, a dőlést és a kormányzást. A kerékpáros egyensúlyának megtartása a szabadságfokok ügyes koordinációját igényli.
- Robotkar: Egy robotkar szabadságfokainak száma a csuklóinak számától és típusától függ. Egy egyszerű robotkarnak is lehet több szabadságfoka, ami lehetővé teszi, hogy komplex mozgásokat végezzen.
A szabadságfokok számának ismerete kulcsfontosságú a szimulációk és a vezérlőrendszerek tervezésében is. A helyes számítás lehetővé teszi a mozgások pontos előrejelzését és a rendszer stabil működésének biztosítását.
A túlhatározott rendszerek olyan rendszerek, ahol a kényszerek száma meghaladja a szabadságfokok számát. Ezekben a rendszerekben belső feszültségek alakulhatnak ki.
Érdemes megemlíteni, hogy a virtuális szabadságfokok is léteznek, amelyek nem valódi mozgásokat képviselnek, hanem matematikai segédeszközök a rendszer leírására. Ezeket gyakran használják komplex rendszerek modellezésekor.
Egyszerű inga és kettős inga
A szabadságfok egy mechanikai rendszer leírásához szükséges független koordináták száma. Egy rendszer mozgásának teljes meghatározásához ennyi változó értékét kell ismernünk.
Nézzük meg ezt az egyszerű inga esetében. Az inga egyetlen pontban rögzített, és egy síkban leng. A mozgásának teljes leírásához elegendő egyetlen szög, az inga függőlegeshez viszonyított szöge. Ez azt jelenti, hogy az egyszerű ingának egy szabadságfoka van.
A helyzet bonyolódik a kettős inga esetében. A kettős inga két, egymáshoz csuklósan kapcsolódó rúd alkot, amelyek egy pontban vannak rögzítve. Itt már nem elég egyetlen szög a rendszer állapotának leírásához. Szükségünk van az első rúd függőlegeshez viszonyított szögére, és a második rúd első rúdhoz viszonyított szögére is. Tehát a kettős ingának két szabadságfoka van.
A kettős inga viselkedése lényegesen bonyolultabb, mint az egyszerű ingáé, és akár kaotikus is lehet, ami azt jelenti, hogy a kis kezdeti eltérések is drasztikusan eltérő mozgásokhoz vezethetnek.
A szabadságfokok száma jelentősen befolyásolja a rendszer viselkedését. Minél több szabadságfoka van egy rendszernek, annál komplexebb és nehezebben modellezhető a mozgása. Ezért a kettős inga sokkal érdekesebb (és kihívást jelentő) tanulmányozni, mint az egyszerű inga.
Gépjármű felfüggesztése
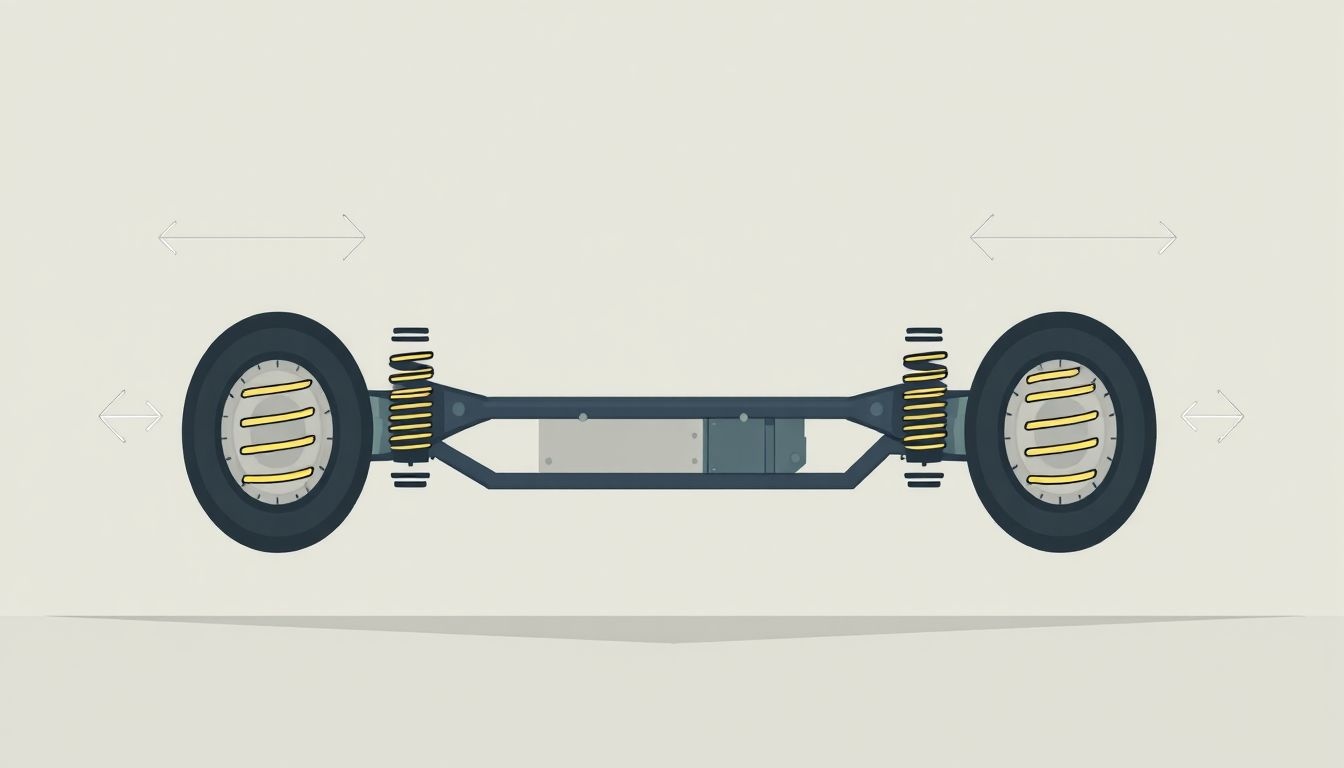
A gépjármű felfüggesztése a karosszéria és a kerekek közötti kapcsolatot biztosítja. A szabadságfokok száma itt azt mutatja meg, hogy hányféleképpen képes mozogni a kerék a karosszériához képest. Egy ideális felfüggesztésnek képesnek kell lennie arra, hogy bizonyos mozgásokat engedélyezzen (például a kerék függőleges elmozdulását a talajegyenetlenségek követésére), miközben más mozgásokat korlátoz (például a karosszéria oldalirányú dőlését kanyarodáskor).
A legtöbb személygépkocsi felfüggesztése tipikusan kevesebb szabadságfokkal rendelkezik, mint amennyi elméletileg lehetséges lenne. Ennek oka az, hogy a mérnököknek kompromisszumot kell kötniük a költség, a komplexitás és a teljesítmény között. Például egy egyszerű merev tengelyes felfüggesztés kevesebb szabadságfokkal rendelkezik, mint egy független kerékfelfüggesztés, de általában olcsóbb és robusztusabb.
A felfüggesztés célja, hogy maximalizálja a kerék tapadását az útfelülethez, ezzel biztosítva a lehető legjobb irányíthatóságot és fékezési teljesítményt, miközben minimalizálja a karosszéria mozgásait a kényelmes utazás érdekében.
A szabadságfokok befolyásolják, hogy a felfüggesztés milyen jól képes elnyelni az útegyenetlenségeket. Minél több szabadságfoka van egy felfüggesztésnek, annál jobban képes szűrni a rezgéseket és a rázkódásokat, de annál bonyolultabb és költségesebb is a rendszer.
A modern felfüggesztési rendszerek, mint például az aktív felfüggesztések, képesek elektronikusan szabályozni a lengéscsillapítást és a rugózást, ezzel dinamikusan változtatva a szabadságfokok hatását a vezetési körülményekhez igazodva. Ez lehetővé teszi a kompromisszumok optimalizálását a kényelem és a teljesítmény között.
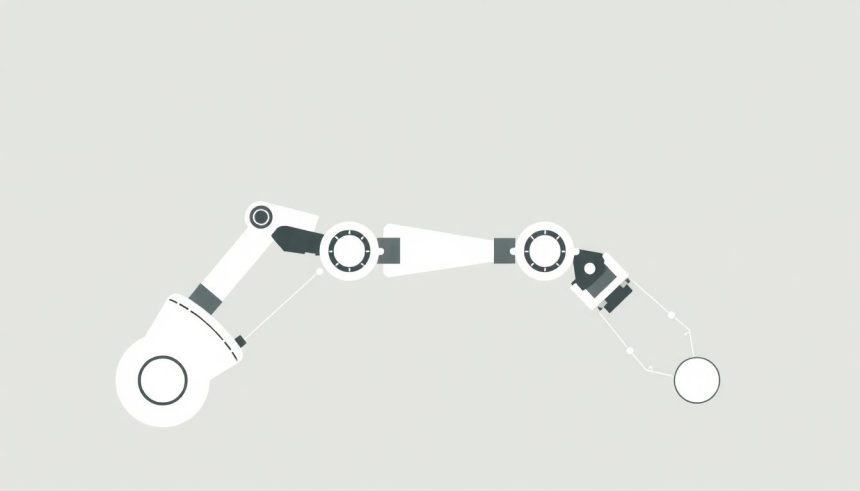
Robotkarok és manipulátorok
A robotkarok és manipulátorok tervezésénél kulcsfontosságú a szabadságfok (Degrees of Freedom, DOF) fogalma. Egyszerűen fogalmazva, a szabadságfok megmutatja, hogy egy robotkar hány független irányban képes mozogni.
Minden tengely, amely mentén a robotkar foroghat vagy elmozdulhat, egy szabadságfokot jelent. Például, egy egyszerű robotkar, amely csak egy tengely körül tud forogni, egyetlen szabadságfokkal rendelkezik. Ezzel szemben egy komplex ipari robotkar, amely képes előre-hátra, fel-le, jobbra-balra mozogni, és emellett több tengely körül forogni is, akár hat vagy több szabadságfokkal is rendelkezhet.
A szabadságfokok száma közvetlenül befolyásolja a robotkar munkaterét és manőverezőképességét. Minél több szabadságfokkal rendelkezik egy robotkar, annál bonyolultabb mozgásokat képes végrehajtani, és annál több helyen érheti el a munkaterületen.
A robotkarok szabadságfokainak optimális megválasztása kritikus fontosságú a tervezési fázisban, mivel ez határozza meg, hogy a robot képes-e elvégezni a kívánt feladatot hatékonyan.
A robotkarok mozgása gyakran kinematikai egyenletekkel írható le, amelyek a szabadságfokokat és a robotkar egyes részeinek pozícióját, illetve orientációját kapcsolják össze. Ezek az egyenletek teszik lehetővé a robotkar irányítását és a kívánt mozgások megtervezését.
A gyakorlatban a robotkarok szabadságfokainak száma a feladat jellegétől függ. Például, egy egyszerű pick-and-place feladathoz elegendő lehet egy három- vagy négy szabadságfokú robotkar, míg egy komplexebb, összeszerelési feladathoz, ahol a robotkarnak több irányból kell hozzáférnie a munkadarabhoz, hat vagy több szabadságfokú robotkarra lehet szükség.
A robotkarok szabadságfokainak növelése nem csak a manőverezőképességet javítja, hanem a vezérlés komplexitását is növeli. Több szabadságfokú robotkarok vezérlése bonyolultabb algoritmusokat igényel, és nagyobb számítási kapacitást.
Párhuzamos mechanizmusok
A párhuzamos mechanizmusok különleges helyet foglalnak el a mechanika világában. A szabadságfok (degrees of freedom, DOF) egy mechanizmus mozgásának leírásához szükséges független paraméterek számát jelenti. Párhuzamos mechanizmusoknál a szabadságfok meghatározása kritikus fontosságú a kívánt mozgás eléréséhez.
A párhuzamos mechanizmusok, ellentétben a soros mechanizmusokkal (pl. robotkarok), több ágon keresztül kapcsolják össze az alapot és a végrehajtó szerszámot (end-effector). Emiatt a szabadságfok meghatározása nem egyszerűen az egyes ízületek szabadságfokainak összege. A kinematikai láncok geometriája és az ízületek korlátozásai jelentősen befolyásolják a rendszer teljes szabadságfokát.
Például, egy Stewart-Gough platform, egy tipikus párhuzamos mechanizmus, hat szabadságfokkal rendelkezik (három transzlációs és három rotációs). Ezt hat lineáris aktuátorral érik el, amelyek a platformot az alaphoz kötik. Azonban nem minden párhuzamos mechanizmus rendelkezik hat szabadságfokkal; a kialakítástól függően lehet kevesebb is.
A párhuzamos mechanizmusok tervezésénél elengedhetetlen a megfelelő szabadságfok biztosítása a kívánt feladat végrehajtásához. A túl kevés szabadságfok korlátozza a mozgást, míg a túl sok bonyolulttá teszi a vezérlést.
A szabadságfok elemzés során figyelembe kell venni az ízületek típusát (pl. forgó, csúszó), azok orientációját, és a kinematikai láncok geometriáját. A cél a rendszer független mozgásainak azonosítása és a redundáns mozgások elkerülése.
A szabadságfok szerepe a robotikában és az automatizálásban
A szabadságfok (DOF) a robotikában és az automatizálásban kulcsfontosságú fogalom. Meghatározza, hogy egy robot vagy mechanizmus hány független módon képes mozogni a térben. Minél több szabadságfokkal rendelkezik egy robot, annál komplexebb mozgásokra képes, és annál jobban tud alkalmazkodni a változó környezethez.
A szabadságfokok alapvetően két típusba sorolhatók: transzlációs (lineáris) és rotációs (szögletes). A transzlációs szabadságfokok a tengelyek mentén történő elmozdulást (x, y, z), míg a rotációs szabadságfokok a tengelyek körüli elfordulást (pl. bólintás, billentés, forgatás) írják le.
Egy tipikus ipari robotkar általában 6 szabadságfokkal rendelkezik: 3 transzlációs és 3 rotációs. Ez lehetővé teszi, hogy a robotkar bármilyen pozíciót és orientációt elérjen a munkaterében. Azonban léteznek egyszerűbb robotok, például lineáris aktuátorok, amelyek csak egy szabadságfokkal rendelkeznek, valamint komplexebb rendszerek, amelyek több szabadságfokkal rendelkeznek, és ezáltal rendkívül összetett feladatok elvégzésére alkalmasak.
A szabadságfokok száma közvetlenül befolyásolja a robot munkaterét és ügyességét. Egy nagyobb munkatér azt jelenti, hogy a robot nagyobb területen képes dolgozni, míg a nagyobb ügyesség lehetővé teszi a komplexebb feladatok, például a tárgyak bonyolult helyzetekben történő megfogását és manipulálását. A robot tervezésekor a szabadságfokok számának megválasztása kulcsfontosságú szempont, amelyet a konkrét alkalmazási terület követelményei határoznak meg.
A robotikában a szabadságfokok száma nem csupán egy technikai specifikáció, hanem a rendszer képességeinek és alkalmazhatóságának alapvető mérőszáma.
Például:
- Egy hegesztőrobotnak pontosan kell követnie a hegesztési vonalat, amihez több szabadságfokra van szüksége.
- Egy pick-and-place robot, amely egyszerűen csak felvesz és áthelyez tárgyakat, kevesebb szabadságfokkal is ellátható.
A szabadságfokok optimalizálása a robotikai tervezés egyik központi kihívása. A túl sok szabadságfok növelheti a rendszer komplexitását és költségeit, míg a túl kevés korlátozhatja a robot képességeit. A megfelelő egyensúly megtalálása elengedhetetlen a hatékony és gazdaságos robotikai megoldások létrehozásához.
A szabadságfok és a mozgástervezés
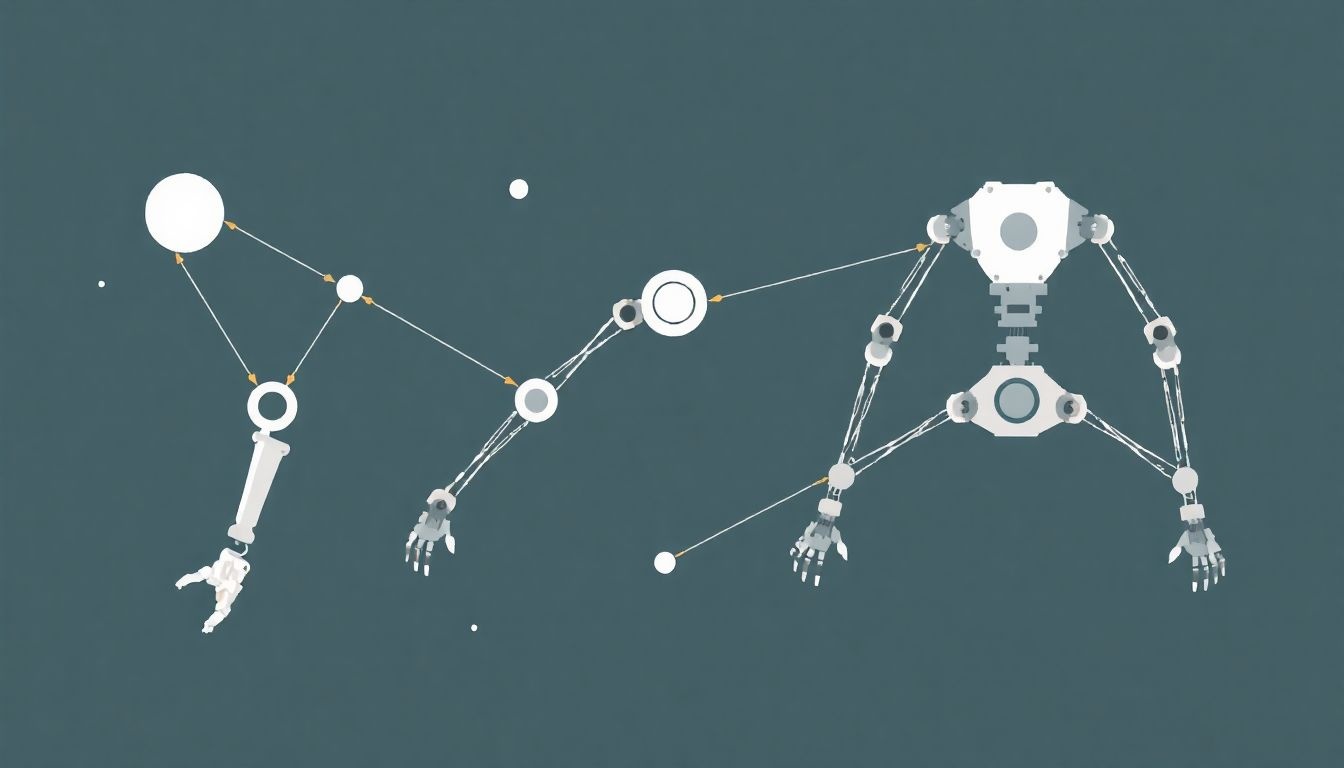
A szabadságfok (degrees of freedom, DOF) egy mechanikai rendszer független mozgásainak számát jelöli. Egyszerűbben fogalmazva, megmutatja, hogy egy objektum hányféleképpen képes mozogni a térben.
A mozgástervezés során a szabadságfok kulcsfontosságú tényező. Egy robotkar például, minél több szabadságfokkal rendelkezik, annál bonyolultabb mozgásokra képes. Egy háromdimenziós térben szabadon mozgó merev testnek 6 szabadságfoka van: 3 a transzláció (x, y, z tengelyek mentén) és 3 a rotáció (a tengelyek körüli elfordulás).
A mozgástervezés algoritmusa a szabadságfokok számának növekedésével jelentősen bonyolódik. Egy egyszerű robotkar esetében a mozgástervezés viszonylag egyszerű, de egy komplex humanoid robot esetében, amely több tucat szabadságfokkal rendelkezik, a mozgástervezés komoly számítási kihívást jelent.
A szabadságfokok száma közvetlenül befolyásolja a mozgástervező algoritmusok komplexitását és a megoldás megtalálásához szükséges időt.
A mozgástervezés során figyelembe kell venni a rendszer korlátozásait is. Ezek a korlátozások csökkenthetik a ténylegesen kihasználható szabadságfokok számát.
Például:
- Egy robotkar, aminek a mozgását falak vagy más objektumok korlátozzák, kevesebb szabadságfokkal rendelkezik, mint ha szabadon mozoghatna.
- Egy autó, ami csak a földön közlekedhet, nem rendelkezik a függőleges irányú mozgás szabadságfokával.
A szabadságfokok meghatározása és kezelése elengedhetetlen a hatékony és biztonságos mozgástervezéshez, különösen komplex robotikai rendszerek esetében. A megfelelő tervezési döntésekkel optimalizálható a rendszer teljesítménye és elkerülhetők a nem kívánt ütközések vagy instabilitások.
A szabadságfok korlátozása a robotokban: biztonság és hatékonyság
A robotok szabadságfokának korlátozása kulcsfontosságú a biztonság és a hatékonyság szempontjából. Bár a magasabb szabadságfok elméletileg nagyobb mozgékonyságot tesz lehetővé, a gyakorlatban ez összetettebb vezérlést és potenciálisan nagyobb hibalehetőséget jelent.
A korlátozás egyik módja a mechanikai tervezés. Például, egy robotkar csuklóinak számának csökkentése csökkenti a lehetséges mozgások számát, ami egyszerűbbé teszi a programozást és a balesetek elkerülését.
Másik megközelítés a szoftveres korlátozás, ahol a vezérlőrendszer korlátozza a robot egyes ízületeinek mozgását. Ez lehetővé teszi a robot számára, hogy elméletileg képes legyen bizonyos mozgásokra, de gyakorlatban a szoftver megakadályozza ezeket, ha azok veszélyesek vagy nem kívánatosak lennének. Ez különösen fontos az ember-robot együttműködésben.
A szabadságfok korlátozása nem feltétlenül jelenti a funkcionalitás csökkenését. A cél a megfelelő egyensúly megtalálása a mozgékonyság és a biztonság között.
Például, egy összeszerelő robotnak lehet, hogy csak néhány szabadságfoka van, de ezeket precízen és megbízhatóan kell tudnia használni. A pontosság és a megbízhatóság gyakran fontosabb, mint a komplex mozgások.
A szabadságfok korlátozása tehát nem pusztán a mozgások számának csökkentését jelenti, hanem egy stratégiai döntést, amely befolyásolja a robot teljesítményét, biztonságát és felhasználhatóságát.
A szabadságfok alkalmazása a virtuális valóságban és a szimulációban
A virtuális valóság (VR) és a szimulációs technológiák terén a szabadságfokok (degrees of freedom, DoF) kulcsfontosságú szerepet játszanak az immerzív élmény megteremtésében. A szabadságfok azt mutatja meg, hogy egy objektum, például egy VR-szemüveget viselő felhasználó feje, hányféleképpen képes mozogni a térben.
Minél több szabadságfokkal rendelkezik egy virtuális objektum, annál realisztikusabban lehet szimulálni a mozgását és interakcióit. Például egy 3DoF-os VR-szemüveg csak a fej elforgatását (dőlés, bólintás, forgatás) követi nyomon, míg egy 6DoF-os rendszer a fej pozíciójának változását is (előre/hátra, jobbra/balra, fel/le). Ez utóbbi sokkal természetesebb mozgásérzetet eredményez.
A magasabb szabadságfokú rendszerek lehetővé teszik, hogy a felhasználó a virtuális térben úgy mozogjon, ahogyan a valóságban is tenné, ami jelentősen növeli az élmény hitelességét és a beleélést.
A szimulációkban a szabadságfokok meghatározzák a modellezett rendszer komplexitását és pontosságát. Egy repülésszimulátorban például a repülőgép szárnyainak mozgása, a hajtóművek teljesítménye és a légköri viszonyok mind különböző szabadságfokokkal rendelkeznek, amelyek együttesen befolyásolják a szimuláció eredményét.
A videojátékokban is fontos szerepet játszanak a szabadságfokok. Egy karakter mozgásának szabadságfoka határozza meg, hogy mennyire szabadon mozoghat a játékos a világban. A magasabb szabadságfokú rendszerek lehetővé teszik a komplexebb mozgásokat és interakciókat, ami javítja a játékélményt.
Azonban a magasabb szabadságfokú rendszerek nagyobb számítási igényt jelentenek. Ezért a fejlesztőknek kompromisszumot kell kötniük a realizmus és a teljesítmény között.
A mozgásérzékelés és a szabadságfok
A szabadságfok egy mechanikai rendszer lehetséges, független mozgásainak számát jelöli. A mozgásérzékelés szempontjából ez kulcsfontosságú, hiszen meghatározza, hogy egy test, például egy robotkar, hányféleképpen tud mozogni a térben.
Egy pontszerű testnek a térben három szabadságfoka van: elmozdulás az x, y és z tengelyek mentén. Egy merev testnek emellett három forgási szabadságfoka is van, a három tengely körül. Így egy merev testnek összesen hat szabadságfoka van.
A mozgásérzékelők, mint például a gyorsulásmérők és giroszkópok, ezeket a szabadságfokokat detektálják. Az adatokból következtetni lehet a test helyzetére, sebességére és orientációjára.
Minél több szabadságfokkal rendelkezik egy rendszer, annál komplexebb a mozgása, és annál több szenzorra van szükség a pontos mozgásérzékeléshez.
Például, egy emberi kéz sokkal több szabadságfokkal rendelkezik, mint egy egyszerű robotkar, ezért a mozgásának érzékelése is sokkal bonyolultabb.
A szabadságfokok száma befolyásolja a mozgásérzékelés pontosságát és a szükséges számítási kapacitást. A mozgásérzékelés során a cél a szabadságfokok meghatározása és azok időbeli változásának követése.
Szimulációs környezetek és a szabadságfokok modellezése
A szimulációs környezetekben a szabadságfokok (DOF) elengedhetetlenek a mozgás és az interakciók pontos modellezéséhez. A DOF azt mutatja meg, hogy egy objektum hány független módon képes mozogni a térben. Például egy merev testnek a háromdimenziós térben 6 DOF-ja van: 3 transzlációs (x, y, z tengelyek mentén) és 3 rotációs (x, y, z tengelyek körül).
A szimuláció során a szabadságfokok korlátozhatók, hogy egyszerűsítsük a modellt, vagy hogy bizonyos fizikai feltételeket szimuláljunk. Például egy csuklós szerkezetben a csuklók korlátozzák a mozgást, ezáltal csökkentve a DOF-ok számát. Minél több DOF-ot veszünk figyelembe, annál pontosabb a szimuláció, viszont annál nagyobb a számítási igény.
A szimulációs szoftverek különböző módszereket kínálnak a DOF-ok kezelésére. Ezek közé tartoznak a következők:
- Explicit megadás: A felhasználó közvetlenül definiálja az egyes objektumok DOF-jait.
- Kényszerek alkalmazása: A szimuláció automatikusan korlátozza a DOF-okat a megadott kényszerek alapján (pl. csuklók, felületek).
- Automatikus DOF-számítás: A szoftver automatikusan meghatározza a DOF-ok számát a modell geometriájából és a kényszerekből.
A robotika területén a DOF-ok kulcsfontosságúak a robotkarok mozgásának tervezéséhez és vezérléséhez. A megfelelő DOF-ok kiválasztása lehetővé teszi a robot számára, hogy elérje a kívánt pozíciót és orientációt a munkaterületen. A virtuális valóságban pedig a felhasználó mozgásának követése és a virtuális avatár mozgásának szimulálása is a DOF-ok pontos modellezését igényli.
A szabadságfokok pontos modellezése kritikus fontosságú a realisztikus és megbízható szimulációkhoz.
A DOF-ok modellezésének pontossága közvetlenül befolyásolja a szimuláció eredményeit. Egy nem megfelelően modellezett rendszer hibás következtetésekhez vezethet. A szimulációs környezetekben a DOF-ok megfelelő kezelése elengedhetetlen a tervezés, az optimalizálás és a vezérlés szempontjából.
A szabadságfok szerepe a biomechanikában
A szabadságfok egy mechanikai rendszerben azt mutatja meg, hogy hány független paraméter szükséges a rendszer helyzetének és konfigurációjának egyértelmű leírásához. A biomechanikában ez kulcsfontosságú, hiszen az emberi test, mint egy komplex mechanikai rendszer, számos ízületből és mozgó részből áll.
Minden ízületnek meghatározott számú szabadságfoka van. Például, a vállízületnek 3 szabadságfoka van (hajlítás/nyújtás, elrablás/közelítés, befelé/kifelé forgatás), ami lehetővé teszi a kar széles körű mozgását. Ezzel szemben, a könyökízületnek tipikusan csak 1 szabadságfoka van (hajlítás/nyújtás).
A szabadságfokok ismerete elengedhetetlen a mozgások elemzéséhez és modellezéséhez. A biomechanikai modellek gyakran használják a szabadságfokokat a testrészek mozgásának leírására és a rájuk ható erők és nyomatékok kiszámítására.
A szabadságfokok korlátozása befolyásolja a mozgásmintázatot és a végrehajtható feladatok körét.
Például, egy sérülés vagy betegség korlátozhatja egy ízület szabadságfokait, ami mozgáskorlátozottsághoz és fájdalomhoz vezethet. A rehabilitáció célja gyakran az elvesztett szabadságfokok visszaszerzése és a normális mozgásmintázat helyreállítása.
A szabadságfokok elemzése segíthet a sportteljesítmény optimalizálásában is. Például, egy sportoló mozgásának elemzésével megállapítható, hogy mely ízületek mozgástartománya korlátozott, és hogyan befolyásolja ez a teljesítményét. A megfelelő edzéssel és technikával növelhető a mozgástartomány és javítható a teljesítmény.
A protézisek és ortézisek tervezése során is figyelembe kell venni a szabadságfokokat. Egy jól megtervezett protézisnek vagy ortézisnek lehetővé kell tennie a felhasználó számára a lehető legtöbb normális mozgást, miközben stabilan tartja és védi az érintett ízületet.
Az emberi test szabadságfokai: ízületek és mozgások
A szabadságfok (degrees of freedom, DOF) a mechanikában egy rendszer, például az emberi test, független mozgásainak számát jelenti. Másképp fogalmazva, megmutatja, hogy egy test hány különböző irányban mozdulhat el vagy fordulhat el a térben.
Az emberi test rendkívül komplex rendszer, melynek szabadságfokai az ízületekben koncentrálódnak. Minden egyes ízület lehetővé teszi bizonyos mozgásokat, melyek mindegyike hozzáadódik a test teljes szabadságfokához. Például a vállízület egy gömbcsukló, ami elvileg három szabadságfokot kínál: hajlítás/nyújtás, elrablás/közelítés és befelé/kifelé forgatás.
Egy ízület szabadságfokainak száma közvetlenül befolyásolja a mozgástartományát és a test rugalmasságát.
Ezzel szemben a könyökízület elsősorban egy zsanérízület, ami főként egy szabadságfokkal rendelkezik: hajlítás és nyújtás. Bár a könyök képes pronációra és szupinációra is, ez a mozgás a csukló és az alkar komplex kölcsönhatásának eredménye.
A gerinc is számos ízületet tartalmaz, melyek mindegyike kis mértékben járul hozzá a test mozgékonyságához. A gerincoszlop egésze lehetővé teszi a hajlítást, nyújtást, oldalra hajlítást és a forgást, bár az egyes csigolyák közötti mozgás korlátozott.
A test teljes szabadságfokának meghatározása rendkívül bonyolult, mivel figyelembe kell venni az összes ízületet és azok kölcsönhatásait. A szabadságfokok ismerete elengedhetetlen a biomechanikai elemzésekhez, a robotika tervezéséhez és a rehabilitációs terápiák kidolgozásához.
Protézisek és exoskeletonok: a szabadságfokok kihívásai
A szabadságfok (degrees of freedom, DOF) egy mechanikai rendszer mozgásának független paramétereinek száma. Egyszerűbben fogalmazva, megmutatja, hogy egy tárgy hányféleképpen képes mozogni a térben. Egy pontnak a síkon két szabadságfoka van (x és y irány), a térben pedig három (x, y és z irány). A forgás is hozzáad szabadságfokokat.
A protézisek és exoskeletonok tervezésénél a szabadságfokok kritikus szerepet játszanak. Egy ideális protézisnek vagy exoskeletonnak képesnek kell lennie utánozni az elveszett vagy gyengült végtag összes természetes mozgását. Minél több szabadságfokkal rendelkezik egy eszköz, annál természetesebb és intuitívabb a használata.
Azonban a több szabadságfok nem mindig jelent jobbat. A komplexitás növekedésével a vezérlés is nehezebbé válik. Egy sok szabadságfokkal rendelkező eszközt nehéz lehet irányítani, különösen akkor, ha a felhasználó nem rendelkezik a megfelelő képzéssel vagy a megfelelő interfész technológiával. A vezérlési algoritmusok bonyolultsága exponenciálisan nő a szabadságfokok számával.
A protézis tervezők célja megtalálni az egyensúlyt a funkcionalitás (minél több szabadságfok) és a könnyű vezérlés (kevesebb szabadságfok vagy intelligens vezérlési rendszer) között.
Például egy kézprotézis esetében a csukló, az ujjak külön-külön mozgatása mind-mind szabadságfokot jelent. A modern protézisek már képesek több szabadságfokot is kezelni, lehetővé téve a felhasználó számára, hogy komplex feladatokat végezzen el, mint például tárgyak megfogása vagy finom mozdulatok végrehajtása.
Az exoskeletonok esetében, amelyek célja a felhasználó erejének növelése vagy a mozgás segítése, a szabadságfokok kérdése hasonlóan fontos. Egy jól megtervezett exoskeleton képes követni a felhasználó természetes mozgását, anélkül, hogy korlátozná azt. A rosszul megtervezett exoskeleton viszont kényelmetlen lehet és akár sérülést is okozhat.
A szabadságfok és a gépészet egyéb területei

A szabadságfok egy mechanikai rendszer független mozgáslehetőségeinek számát jelenti. Gépészeti tervezés során kulcsfontosságú annak megértése, hogy egy alkatrész vagy szerkezet milyen mozgásokat végezhet, és ezek a mozgások hogyan befolyásolják a rendszer működését.
Például, egy merev test a térben hat szabadságfokkal rendelkezik: három eltolási (x, y, z tengelyek mentén) és három forgási (az x, y, z tengelyek körül) mozgással. A valóságban azonban a legtöbb gépészeti rendszerben a mozgásokat korlátozzák, például csapágyakkal, csuklókkal vagy más mechanizmusokkal.
A szabadságfokok ismerete elengedhetetlen a kinematikai és dinamikai analízisekhez, melyekkel a szerkezetek mozgását és az azokra ható erőket vizsgáljuk.
A szabadságfokok csökkentése (például egy csuklópánttal) a szerkezet stabilitását növelheti, de korlátozhatja a funkcionalitását is. Ezzel szemben a túl sok szabadságfok instabilitáshoz vagy nem kívánt mozgásokhoz vezethet.
A robotikában a szabadságfokok száma meghatározza a robot karjának manipulációs képességeit. Minél több szabadságfoka van egy robotnak, annál komplexebb mozgásokra képes. A gépszerkezetek tervezésekor pedig a szabadságfokok pontos meghatározása biztosítja a kívánt működést és a megfelelő stabilitást.
A szabadságfokok fogalma szorosan kapcsolódik a kényszerekhez. A kényszerek olyan feltételek, amelyek korlátozzák a rendszer mozgását, és ezáltal csökkentik a szabadságfokok számát. A csapágyak, csuklók és vezetők mind kényszereket valósítanak meg.
A szabadságfok fogalma a statikában
A szabadságfok a statikában egy test vagy rendszer lehetséges független mozgásainak számát jelenti. Ezek a mozgások lehetnek transzlációk (eltolódások) valamelyik tengely mentén és rotációk (elfordulások) valamelyik tengely körül.
Egy merev test a térben hat szabadságfokkal rendelkezik: három transzláció (x, y, z tengelyek mentén) és három rotáció (x, y, z tengelyek körül). A kényszerek, például csuklók vagy támaszok, korlátozzák ezeket a mozgásokat, és ezzel csökkentik a szabadságfokok számát.
A szabadságfokok száma alapvetően meghatározza, hogy egy statikai probléma statikailag határozott, határozatlan vagy instabil.
Például, egy síkbeli tartó, amely két csuklóval van megtámasztva, három szabadságfokkal rendelkezik (két transzláció és egy rotáció). Ha a támaszok rögzítettek, a szabadságfokok száma nulla lesz, ami azt jelenti, hogy a tartó mozdulatlan.
A szabadságfokok ismerete elengedhetetlen a szerkezetek viselkedésének elemzéséhez és a terhelések hatására kialakuló erők és nyomatékok meghatározásához.
A szabadságfok fogalma a dinamikában
A szabadságfok egy mechanikai rendszer lehetséges független mozgásainak számát jelöli. Másképpen fogalmazva, az a minimális számú koordináta, amellyel egyértelműen leírható a rendszer konfigurációja.
Egy szabadon mozgó merev testnek a térben hat szabadságfoka van: három transzlációs (x, y, z tengelyek mentén) és három rotációs (a három tengely körüli forgás). A szabadságfokok száma csökkenhet, ha a rendszer valamilyen módon korlátozott, például csuklókkal vagy sínekkel.
A szabadságfokok száma kulcsfontosságú a mechanikai rendszerek dinamikai viselkedésének elemzésekor.
A szabadságfokok meghatározása elengedhetetlen a mozgásegyenletek felírásához és a rendszer viselkedésének szimulálásához. Minél több szabadságfoka van egy rendszernek, annál komplexebb a viselkedése, és annál nehezebb a matematikai leírása.
Például, egy inga egy szabadságfokkal rendelkezik (a függőlegeshez viszonyított szög). Egy autó felfüggesztése jóval több szabadságfokkal rendelkezik, hiszen a karosszéria mozoghat fel-le, előre-hátra, oldalra, és foroghat is a különböző tengelyek körül.
A szabadságfok és a rezgések
A szabadságfok egy mechanikai rendszer független koordinátáinak számát jelenti, amelyek szükségesek a rendszer konfigurációjának teljes leírásához. A rezgések szempontjából ez azt jelenti, hogy hányféleképpen képes egy objektum vagy rendszer mozogni.
Például, egy pontszerű tömeg a síkon két szabadságfokkal rendelkezik, mivel a helyzetét két koordinátával (x, y) tudjuk meghatározni. Ha ez a tömeg egy rugóhoz van rögzítve, akkor rezgéseket végezhet e két irányban.
Minél több szabadságfokkal rendelkezik egy rendszer, annál összetettebbek lehetnek a rezgési módusai.
Egy merev test a térben hat szabadságfokkal rendelkezik: három transzlációs (x, y, z) és három rotációs (a tengelyek körül). Ennek megfelelően a rezgései is sokkal bonyolultabbak lehetnek, mint egy egyszerű pontszerű tömegé. A szabadságfokok száma közvetlenül befolyásolja a rendszer rezonanciafrekvenciáit és a rezgések terjedésének módját.
A Lagrange-formalizmus és a szabadságfokok
A Lagrange-formalizmus a mechanikai rendszerek leírásának egy hatékony eszköze, melynek alapvető fogalma a szabadságfok (degrees of freedom). A szabadságfok megadja, hogy hány független változó szükséges a rendszer konfigurációjának egyértelmű meghatározásához. Másképpen fogalmazva, ez a minimális számú koordináta, amivel a rendszer minden lehetséges helyzete egyértelműen leírható.
A szabadságfokok száma kulcsfontosságú a Lagrange-függvény felírásához, hiszen a Lagrange-függvény a rendszer mozgási és potenciális energiájának különbségeként definiálható, és ez a különbség a szabadságfokokhoz tartozó koordináták és azok időbeli deriváltjai függvényében fejezhető ki.
Például, egy síkon mozgó pontrendszer esetén, ha N számú pont van, akkor a rendszernek 2N szabadságfoka van, mivel minden pont helyzetét két koordinátával (x, y) kell megadni. Ha a pontok között kényszerfeltételek vannak (pl. merev testet alkotnak), akkor a szabadságfokok száma csökken.
A Lagrange-formalizmus előnye, hogy a kényszerfeltételeket implicit módon kezeli, így nem kell külön foglalkozni a kényszererőkkel. Ezzel a módszerrel a mozgásegyenletek felírása egyszerűbbé és átláthatóbbá válik. A szabadságfokok helyes meghatározása elengedhetetlen a Lagrange-egyenletek helyes felírásához és a rendszer mozgásának pontos leírásához.
A Hamilton-formalizmus és a szabadságfokok
A Hamilton-formalizmusban a szabadságfokok kulcsszerepet játszanak a rendszer állapotának leírásában. A szabadságfok azt adja meg, hogy hány független változó szükséges a rendszer konfigurációjának egyértelmű meghatározásához.
Egy N részecskéből álló rendszer esetén, ha a részecskék mozgását nem korlátozza semmi, akkor 3N szabadságfoka van, mivel minden részecskének három koordinátára (x, y, z) van szüksége a térben való helyzetének leírásához.
A Hamilton-formalizmus a szabadságfokokat általánosított koordináták (qi) és általánosított impulzusok (pi) segítségével kezeli. Minden egyes szabadságfokhoz tartozik egy általánosított koordináta és egy hozzá tartozó általánosított impulzus. A Hamilton-függvény (H) ezeknek a változóknak a függvénye, és a rendszer teljes energiáját fejezi ki.
A szabadságfokok száma alapvetően meghatározza a Hamilton-függvény alakját és ezáltal a rendszer dinamikáját.
Kényszerek jelenléte csökkentheti a szabadságfokok számát. Például, ha egy részecske egy adott felületen kell mozogjon, akkor a felület egyenlete egy kényszert jelent, és a szabadságfokok száma csökken.
A Hamilton-egyenletek, amelyek a rendszer időbeli fejlődését írják le, 2n számú elsőrendű differenciálegyenletet alkotnak, ahol n a szabadságfokok száma. Ezek az egyenletek a következők:
- dqi/dt = ∂H/∂pi
- dpi/dt = -∂H/∂qi
Ezek az egyenletek mutatják, hogy a rendszer dinamikája szorosan összefügg a Hamilton-függvény deriváltjaival az általánosított koordináták és impulzusok szerint, ami ismételten a szabadságfokok központi szerepét hangsúlyozza.
A szabadságfokok és a numerikus módszerek a mechanikában
A szabadságfok (degrees of freedom, DOF) egy mechanikai rendszerben azt adja meg, hogy hány független paraméterre van szükség a rendszer helyzetének egyértelmű meghatározásához. Egyszerűbben fogalmazva: hányféleképpen mozoghat a rendszer.
Például, egy síkon mozgó pontnak két szabadságfoka van (x és y koordináták), míg a térben mozgó pontnak három (x, y és z koordináták). Egy merev testnek a térben hat szabadságfoka van: három transzlációs (x, y, z irányú elmozdulás) és három rotációs (x, y, z tengely körüli elfordulás).
A szabadságfokok száma kulcsfontosságú a mechanikai rendszerek modellezésében és szimulációjában, különösen a numerikus módszerek alkalmazásakor.
A numerikus módszerek, mint például a végeselem-módszer (FEM), a szabadságfokok mentén diszkretizálják a rendszert. Minél több szabadságfokot veszünk figyelembe, annál pontosabb a szimuláció, de annál nagyobb a számítási igény is.
A megfelelő számú szabadságfok kiválasztása kritikus fontosságú a pontos és hatékony szimulációk eléréséhez. Túl kevés szabadságfok pontatlan eredményekhez vezethet, míg túl sok feleslegesen növelheti a számítási időt.
A szabadságfokok fogalma alapvető a robotikában, a szerkezettervezésben és a dinamikai szimulációkban is. A rendszerek viselkedésének megértése és előrejelzése nagymértékben függ a szabadságfokok helyes kezelésétől.
Végsőelem-módszer (Finite Element Method – FEM) és a szabadságfokok
A szabadságfok (DOF) a végeselem-módszer (FEM) egyik alapvető fogalma. A szabadságfokok egy rendszer független változóinak számát jelölik, amelyek szükségesek a rendszer konfigurációjának teljes leírásához. Mechanikai rendszerekben ezek általában transzlációs (eltolódási) és rotációs (elfordulási) mozgások. A FEM modellben minden csomóponthoz (node) hozzárendelünk bizonyos számú szabadságfokot.
Egy 2D-s problémában például egy csomópontnak lehet két transzlációs (x és y irányú elmozdulás) és egy rotációs szabadságfoka (a z tengely körüli elfordulás). Egy 3D-s problémában ez a szám hatra nőhet: három transzlációs és három rotációs szabadságfok.
A végeselem-módszer pontossága nagymértékben függ a használt elemtípustól és a szabadságfokok számától.
A szabadságfokok száma közvetlenül befolyásolja a számítási igényt. Minél több a szabadságfok, annál nagyobb a mátrixméret, és annál több számítási idő szükséges a megoldáshoz. Ugyanakkor, a túl kevés szabadságfok alulreprezentálhatja a valós viselkedést, pontatlan eredményekhez vezetve. A megfelelő számú szabadságfok kiválasztása kulcsfontosságú a pontos és hatékony szimulációhoz.
A szabadságfokok korlátozása (constraint) is fontos szerepet játszik a FEM-ben. Például, egy rögzített tartó csomópontjainál minden szabadságfok (eltolódás és elfordulás) zérussá van kényszerítve, ezzel modellezve a rögzítést.
A szabadságfok és a mesterséges intelligencia
A szabadságfok a mechanikában azt jelenti, hogy egy rendszer, például egy robotkar, hányféleképpen képes mozogni. Minél több szabadságfoka van, annál komplexebb mozgásra képes.
A mesterséges intelligencia szempontjából a szabadságfokok kezelése kulcsfontosságú. Egy robotnak, amelynek sok szabadságfoka van, sokkal nehezebb irányítani a mozgását, mint egy egyszerűbb robotnak.
A mesterséges intelligencia feladata, hogy olyan algoritmusokat hozzon létre, amelyek képesek hatékonyan vezérelni a sok szabadságfokkal rendelkező rendszereket.
Gondoljunk egy emberi kézre. Rengeteg szabadságfoka van, ami lehetővé teszi a finommotoros mozgásokat. A mesterséges intelligenciának az a célja, hogy hasonlóan komplex mozgásokat tudjon vezérelni robotoknál, ehhez pedig a szabadságfokok pontos ismerete és kezelése elengedhetetlen.
A gépi tanulás és a mélytanulás módszerei segítenek a robotoknak megtanulni, hogyan használják ki a szabadságfokaikat a kívánt feladat elvégzéséhez. Például, egy robotkar megtanulhatja, hogyan kell egy poharat megfogni anélkül, hogy összetörné, amihez a szabadságfokok koordinált használatára van szükség.
A megerősítéses tanulás és a szabadságfokok
A megerősítéses tanulásban (RL) a szabadságfokok a döntéshozó ügynök rendelkezésére álló lehetséges akciók számát jelentik egy adott állapotban. Minél több szabadságfoka van az ügynöknek, annál komplexebb stratégiákat valósíthat meg, de annál nehezebb is megtanulnia a optimális viselkedést.
Képzeljünk el egy robotot, amelynek az a feladata, hogy eljusson egy adott pontba. Ha a robot csak előre és hátra tud menni, kevés szabadságfoka van. Ha azonban képes oldalra mozogni, forogni és a sebességét is szabályozni, a szabadságfokai jelentősen megnőnek. A több szabadságfok potenciálisan jobb teljesítményt tesz lehetővé, de a tanulási folyamat is bonyolultabbá válik.
A megerősítéses tanulás során a szabadságfokok korlátozása néha segíthet a tanulási folyamat felgyorsításában, mivel csökkenti a keresési teret.
A megfelelő akciótér kialakítása kulcsfontosságú az RL alkalmazásokban. Túl kevés szabadságfok korlátozhatja az ügynök képességeit, míg túl sok szabadságfok megnehezítheti a tanulást és növelheti a számítási igényt.
A szabadságfok fogalmának kiterjesztése más területekre
A mechanikai szabadságfok fogalma, amely egy rendszer független mozgáslehetőségeit írja le, túlnő a mérnöki alkalmazásokon. A statisztikában például a szabadságfok azt mutatja meg, hogy egy adathalmazban hány érték változhat szabadon, miután bizonyos korlátozásokat figyelembe vettek. Ez kulcsfontosságú a statisztikai tesztek, mint például a t-próba vagy a khi-négyzet próba elvégzéséhez, mivel befolyásolja az eredmények pontosságát.
A pénzügyekben a szabadságfok az eszközök közötti korrelációt is jellemezheti egy portfólióban. Minél alacsonyabb a korreláció (tehát minél nagyobb a szabadságfok), annál jobban diverzifikált a portfólió, és annál kevésbé van kitéve az egyedi eszközök teljesítményének.
A szabadságfok fogalma átvitt értelemben használható a döntéshozatalban is, ahol a rendelkezésre álló választási lehetőségek számát jelenti.
A robotikában is fontos szerepet játszik, ahol a robotkarok mozgásának tervezésekor veszik figyelembe, hogy hány tengely mentén tud a robot mozogni. Minél több a szabadságfok, annál komplexebb mozgásokra képes a robot, de annál nehezebb a mozgás tervezése és vezérlése.
Az ökonometriában a szabadságfok a regressziós modellben szereplő paraméterek számának és a megfigyelések számának különbsége. Ez befolyásolja a becslések pontosságát és a statisztikai következtetések érvényességét.
A szabadságfok a statisztikában
A statisztikában a szabadságfok azt mutatja meg, hogy egy statisztikai számítás során hány érték változhat szabadon anélkül, hogy a számítás eredménye megváltozna. Gyakran az elemszám és a becsült paraméterek számának különbsége adja meg.
Például, ha 10 adatunk van és kiszámítjuk az átlagot, akkor 9 adat szabadon változhat, de a 10. adatnak olyannak kell lennie, hogy az átlag helyes maradjon. Ebben az esetben a szabadságfok 9.
A szabadságfok kulcsfontosságú a statisztikai tesztek (például t-próba, khí-négyzet próba) elvégzéséhez, mivel befolyásolja a p-érték kiszámítását és ezáltal a statisztikai szignifikancia megítélését.
A helytelen szabadságfok használata hibás következtetésekhez vezethet. A szabadságfok fogalma segít a mintából származó információk pontosabb felhasználásában a populációra történő következtetéshez.
A szabadságfok a termodinamikában
A termodinamikában a szabadságfok egy molekula energia tárolásának független módjait jelenti. Ezek lehetnek transzlációs (mozgás), rotációs (forgás) és vibrációs módok.
Egyatomos gázoknak, mint az argonnak, általában csak 3 transzlációs szabadságfoka van. Kétatomos gázok, mint az oxigén, rendelkeznek 3 transzlációs, 2 rotációs és (magas hőmérsékleten) 1 vibrációs szabadságfokkal.
A szabadságfokok száma közvetlenül befolyásolja a gázok hőkapacitását, mivel minden szabadságfok hozzájárul az átlagos energiához.
A kiegyenlítő elv szerint az energia egyenletesen oszlik el a szabadságfokok között. Ez az elv magyarázza, hogy a hőmérséklet emelkedésével a molekulák egyre több vibrációs módot aktiválnak.
A szabadságfok fogalmának szemléltetése példákon keresztül
A szabadságfok egy mechanikai rendszer lehetséges független mozgásainak számát jelöli. Másképp fogalmazva, azt mutatja meg, hogy hány független paraméter szükséges a rendszer helyzetének egyértelmű meghatározásához.
Vegyünk egy egyszerű példát: egy pontszerű test, amely egy síkon mozoghat. Ennek a testnek két szabadságfoka van, mert a helyzetét két koordináta (x és y) határozza meg. Ha a test térben mozoghatna, akkor három szabadságfoka lenne (x, y és z koordináták).
A szabadságfok fogalma kulcsfontosságú a mechanikai rendszerek viselkedésének megértéséhez és modellezéséhez.
Egy merev test esetében a helyzetének meghatározásához nem csak a test középpontjának helyzetét kell ismernünk, hanem a test orientációját is. A térben mozgó merev testnek hat szabadságfoka van: három a középpont helyzetének (x, y, z) és három a test orientációjának (például Euler-szögek).
A szabadságfokok számát korlátozhatják kényszerek. Például, ha egy test egy síkban mozog, de egy adott egyenesen kell maradnia, akkor csak egy szabadságfoka van, mert a helyzetét egyetlen koordináta határozza meg.
Nézzünk néhány további példát:
- Egy inga: egy szabadságfoka van, a kitérési szög.
- Egy autó: ideális esetben három szabadságfoka van (előre-hátra mozgás, jobbra-balra mozgás, forgás a függőleges tengely körül).
- Egy robotkar: a szabadságfokok száma az ízületek számától függ. Minden ízület egy újabb szabadságfokot ad hozzá.
Fontos, hogy a szabadságfokok számának meghatározása a rendszer modellezésének pontosságától függ. Például egy autó esetében figyelembe vehetjük a felfüggesztés rugalmasságát is, ami növeli a szabadságfokok számát.
Gyakorlati példák a mindennapi életből
A szabadságfok a mindennapi életben is tetten érhető. Gondoljunk például egy autó mozgására. Előre-hátra haladhat, jobbra-balra fordulhat, és a felfüggesztésnek köszönhetően fel-le is mozoghat bizonyos mértékben. Ez három szabadságfokot jelent a térben való elmozdulásra vonatkozóan.
Egy másik példa az emberi kar. A váll lehetővé teszi a kar körkörös mozgását, a könyök a hajlítást és nyújtást, a csukló pedig a forgatást. Minden egyes ízület növeli a kar szabadságfokát, ami lehetővé teszi a komplex mozgásokat.
Minél több szabadságfokkal rendelkezik egy rendszer, annál összetettebb és változatosabb mozgásokra képes.
A zsanér egy egyszerű példa, mely egyetlen szabadságfokkal rendelkezik: a forgással. Ezzel szemben egy gömbcsukló sokkal több szabadságfokot kínál, lehetővé téve a háromdimenziós mozgást.
Akár egy robotkar tervezésénél, akár egy szék ergonómiájának megtervezésénél, a szabadságfokok ismerete kulcsfontosságú a kívánt mozgás és funkcionalitás eléréséhez.
Gyakorlati példák a mérnöki gyakorlatból
A szabadságfokok a mérnöki tervezés során kritikus szerepet játszanak. Például egy autó futóművének tervezésekor figyelembe kell venni a kerekek felfüggesztésének szabadságfokait. A túl sok szabadságfok instabilitáshoz vezethet, míg a túl kevés a mozgás korlátozásához.
Egy robotkar tervezésénél a csuklópontok száma és típusa határozza meg a kar szabadságfokainak számát. Minél több szabadságfokkal rendelkezik a kar, annál komplexebb mozgásokra képes, de annál bonyolultabb a vezérlése is.
A hídépítésnél a szerkezet elemeinek csatlakozásai jelentik a szabadságfokokat. A merev kapcsolatok kevesebb szabadságfokot eredményeznek, de nagyobb terhelést bírnak, míg a csuklós kapcsolatok több szabadságfokot tesznek lehetővé, de kevésbé terhelhetőek.
A repülőgép szárnyának tervezésekor a csűrők, a féklapok és a magassági kormányok mind a szárny szabadságfokait növelik, lehetővé téve a pilóta számára a gép irányítását. Ezen elemek megfelelő tervezése elengedhetetlen a repülés biztonságához.
Egy csuklós busz tervezésénél a csukló lehetővé teszi a busz számára, hogy szűk kanyarokban is manőverezni tudjon. A csukló szabadságfokai azonban stabilitási problémákat is okozhatnak, ezért a tervezés során gondos mérlegelés szükséges.