Lineáris regresszió (linear regression): a statisztikai modell magyarázata és gyakorlati működése

A lineáris regresszió egy széles körben alkalmazott statisztikai módszer, melynek célja, hogy egy vagy több független változó (magyarázó változó) és egy függő változó (célváltozó) közötti lineáris kapcsolatot modellezze. Alapvető feltevése, hogy a függő változó értéke lineárisan függ a független változók értékeitől. Ez azt jelenti, hogy az összefüggés egy egyenes vonallal (egyszerű lineáris regresszió) vagy egy hiperfelülettel (többszörös lineáris regresszió) ábrázolható.

A modell lényege, hogy a legjobban illeszkedő egyenest vagy hiperfelületet keresi, mely minimalizálja a tényleges értékek és a modell által jósolt értékek közötti különbséget. Ezt a különbséget hibának vagy reziduumnak nevezzük. A leggyakrabban használt módszer a legkisebb négyzetek módszere, mely a reziduumok négyzetösszegét minimalizálja.

A lineáris regresszió lehetővé teszi, hogy előrejelzéseket készítsünk a függő változó értékeire a független változók értékeinek ismeretében.

Gyakorlati alkalmazásai rendkívül sokrétűek. Például:

• Gazdaságban: Értékesítési adatok előrejelzése marketing költések alapján.
• Orvostudományban: Gyógyszeradagolás optimalizálása a beteg jellemzői alapján.
• Pénzügyekben: Részvényárfolyamok becslése makrogazdasági mutatók alapján.

A lineáris regresszió használata során figyelembe kell venni bizonyos feltételezéseket, mint például a hibatagok normalitása és a változók közötti linearitás. Ezen feltételek megsértése esetén a modell pontossága és megbízhatósága csökkenhet. A modell teljesítményét különböző metrikákkal értékelhetjük, mint például az R-négyzet (R²), mely azt mutatja meg, hogy a függő változó varianciájának mekkora részét magyarázza a modell.

A lineáris regresszió matematikai modellje: egyenletek és paraméterek

A lineáris regresszió egy statisztikai módszer, ami egy vagy több független változó (magyarázó változó) és egy függő változó (célváltozó) közötti lineáris kapcsolatot modellezi. A modell lényege, hogy a függő változó értékeit megpróbáljuk megjósolni a független változók értékei alapján.

A legegyszerűbb esete az egyszerű lineáris regresszió, ahol csak egy független változó van. Ennek matematikai modellje a következőképpen írható le:

y = β₀ + β₁x + ε

Ahol:

• y a függő változó.
• x a független változó.
• β₀ a metszéspont (intercept), ami azt az értéket jelenti, ahol a regressziós egyenes metszi az y tengelyt. Gyakorlatban ez azt jelenti, hogy ha x értéke nulla, akkor y várható értéke β₀.
• β₁ a meredekség (slope), ami azt mutatja, hogy a függő változó mennyivel változik, ha a független változó egy egységgel nő.
• ε a hiba tag (error term), ami a modell által nem magyarázott véletlenszerű eltéréseket reprezentálja. Ez azért van, mert a valóságban a kapcsolat sosem tökéletesen lineáris.

A többszörös lineáris regresszió esetében több független változó is szerepel a modellben. Az egyenlet ekkor a következőképpen alakul:

y = β₀ + β₁x₁ + β₂x₂ + … + βₙxₙ + ε

Ahol:

• x₁, x₂, …, xₙ a független változók.
• β₁, β₂, …, βₙ a hozzájuk tartozó meredekségek (koefficiensek). Minden egyes βᵢ azt mutatja, hogy a függő változó mennyivel változik, ha az xᵢ független változó egy egységgel nő, miközben a többi független változó értéke állandó.

A lineáris regresszió célja a β₀, β₁, β₂, …, βₙ paraméterek (koefficiensek) becslése a rendelkezésre álló adatok alapján. A becslés általában a legkisebb négyzetek módszerével (Least Squares Method) történik, ami a hiba tagok négyzetösszegének minimalizálására törekszik. A modell jóságát különböző statisztikai mutatók (például R-négyzet, p-érték) segítségével lehet értékelni.

A gyakorlatban a szoftverek automatikusan elvégzik a paraméterek becslését és a modell értékelését. A felhasználónak a megfelelő adatok előkészítése és a modell eredményeinek értelmezése a feladata.

A legkisebb négyzetek módszere (Least Squares Method): A paraméterek becslése

A legkisebb négyzetek módszere (Least Squares Method) a lineáris regresszió egyik legelterjedtebb és legfontosabb eszköze a modell paramétereinek becslésére. Célja, hogy megtalálja azt az egyenest (vagy hiperfelületet több változó esetén), amely a legjobban illeszkedik a rendelkezésre álló adatokra. A „legjobban illeszkedik” itt azt jelenti, hogy minimalizáljuk az adatok és a regressziós egyenes közötti eltéréseket, azaz a hibákat.

A módszer alapelve a hibák négyzetösszegének minimalizálása. A hibák (reziduálisok) az egyes adatpontok tényleges értékei és a regressziós egyenes által jósolt értékek közötti különbségek. Négyzetre emeljük ezeket a különbségeket, hogy a negatív és pozitív eltérések ne kompenzálják egymást, és hogy a nagyobb eltérések nagyobb súllyal szerepeljenek a minimalizálási folyamatban.

A lineáris regressziós modell egyenlete általában a következő formában írható fel: y = β₀ + β₁x + ε, ahol:

• y a függő változó (a megjósolni kívánt érték).
• x a független változó (a prediktor).
• β₀ a tengelymetszet (az egyenes y tengellyel való metszéspontja).
• β₁ a meredekség (az egyenes iránytangense).
• ε a hiba tag (a modell által nem magyarázott eltérés).

A legkisebb négyzetek módszerének célja, hogy megtalálja a β₀ és β₁ paraméterek optimális értékeit, amelyek minimalizálják a ∑(y_i – (β₀ + β₁x_i))² kifejezést, ahol az összegzés az összes i adatpontra vonatkozik.

A paraméterek becslése analitikusan történhet a deriváltak segítségével. A négyzetösszeg deriváltjait nullával egyenlővé téve, majd az egyenletrendszert megoldva kapjuk meg a legkisebb négyzetek becsléseit a β₀ és β₁ paraméterekre. Ezek a becslések a következőképpen fejezhetők ki:

• β₁ = Cov(x, y) / Var(x), ahol Cov(x, y) a x és y változók kovarianciája, Var(x) pedig a x változó varianciája.
• β₀ = ȳ – β₁x̄, ahol ȳ az y változó átlaga, x̄ pedig a x változó átlaga.

A gyakorlatban a paraméterek becslésére gyakran használnak statisztikai szoftvereket (pl. R, Python, SPSS). Ezek a szoftverek implementálják a legkisebb négyzetek módszerét, és automatikusan kiszámítják a paraméterek becsléseit, valamint a modell egyéb statisztikai mutatóit (pl. R², p-értékek).

Fontos megjegyezni, hogy a legkisebb négyzetek módszere bizonyos feltételezésekkel él, mint például a hibák normalitása, állandó varianciája és függetlensége. Ezen feltételezések megsértése esetén a becslések pontossága és megbízhatósága veszélybe kerülhet.

A költségfüggvény (Cost Function) szerepe a lineáris regresszióban

A lineáris regresszió lényege, hogy egy egyenest illesszünk az adatokra, ami a lehető legjobban reprezentálja a változók közötti kapcsolatot. A költségfüggvény (Cost Function) kulcsszerepet játszik ebben a folyamatban. Ez a függvény számszerűsíti, hogy mennyire „jó” a modellünk, azaz mennyire pontosan jósolja meg a bemeneti adatokhoz tartozó kimeneti értékeket.

A költségfüggvény általában a négyzetes hiba (Mean Squared Error – MSE) valamilyen formája. Ez azt jelenti, hogy minden egyes adatpontra kiszámoljuk a modell által jósolt érték és a valós érték közötti különbséget (a hibát), majd ezt a hibát négyzetre emeljük. Az összes adatpontra kapott négyzetes hibák átlaga adja a költségfüggvény értékét. Minél kisebb ez az érték, annál jobban illeszkedik a modell az adatokra.

A lineáris regresszió célja a költségfüggvény minimalizálása.

Különböző optimalizációs algoritmusok, mint például a gradiens módszer (Gradient Descent), használatosak a költségfüggvény minimumának megtalálására. Ezek az algoritmusok iteratívan módosítják a modell paramétereit (az egyenes meredekségét és tengelymetszetét) addig, amíg a költségfüggvény értéke már nem csökken tovább jelentősen.

A költségfüggvény nem csak a modell illeszkedésének mérésére szolgál, hanem a modell komplexitásának kezelésére is. Bizonyos költségfüggvények büntetik a túl bonyolult modelleket (pl. a túl nagy meredekségű egyeneseket), ezáltal megelőzve a túlillesztést (overfitting), amikor a modell túlságosan is a tanító adatokra van optimalizálva, és nem képes jól teljesíteni új, ismeretlen adatokon.

A gradiens ereszkedés (Gradient Descent) algoritmusa: Optimalizálás a lineáris regresszióban

A lineáris regresszió során a cél a legjobb illeszkedő egyenes megtalálása az adathalmazra. Ez az egyenes leírja a független változó(k) és a függő változó közötti kapcsolatot. A „legjobb illeszkedés” meghatározásához szükségünk van egy költségfüggvényre, amely számszerűsíti, hogy mennyire „rossz” az adott egyenes. A lineáris regresszióban gyakran használt költségfüggvény a négyzetes hiba összege (MSE – Mean Squared Error), amely az előrejelzett és a tényleges értékek közötti különbségek négyzeteinek átlaga.

A gradiens ereszkedés egy iteratív optimalizációs algoritmus, amelyet a költségfüggvény minimumának megtalálására használunk. A lineáris regresszió kontextusában ez azt jelenti, hogy a gradiens ereszkedés segít megtalálni a legoptimálisabb súlyokat (meredekséget és tengelymetszetet) a lineáris egyenlethez, amelyek minimalizálják a költségfüggvény értékét.

Az algoritmus a következőképpen működik:

1. Kezdeti értékek választása: Véletlenszerűen vagy valamilyen heurisztika alapján kiválasztunk kezdeti értékeket a súlyokhoz.
2. Gradiens kiszámítása: Kiszámítjuk a költségfüggvény gradiensét a súlyok szerint. A gradiens megmutatja a legmeredekebb emelkedés irányát a költségfüggvényben.
3. Súlyok frissítése: A súlyokat a gradiens ellentétes irányába mozdítjuk el egy bizonyos mértékben, amit tanulási rátának nevezünk. A tanulási ráta meghatározza, hogy mekkora lépésekkel haladunk a minimum felé.
4. Iteráció: A 2. és 3. lépéseket addig ismételjük, amíg a költségfüggvény értéke nem csökken eléggé, vagy amíg egy előre meghatározott számú iterációt el nem érünk.

A gradiens ereszkedés lényege, hogy a költségfüggvény gradiensét használva „ereszkedünk le” a függvény „völgyébe”, azaz a minimumába, ahol a hibák a legkisebbek.

A tanulási ráta kritikus paraméter. Túl nagy tanulási ráta esetén az algoritmus átugorhatja a minimumot és divergálhat. Túl kicsi tanulási ráta esetén az algoritmus lassan konvergálhat, vagy beleragadhat egy lokális minimumba.

A gyakorlatban a gradiens ereszkedésnek több változata is létezik, például a batch gradiens ereszkedés (amely az összes adaton számítja ki a gradienst), a sztochasztikus gradiens ereszkedés (amely minden egyes adaton számítja ki a gradienst) és a mini-batch gradiens ereszkedés (amely egy kisebb adathalmazon számítja ki a gradienst). A sztochasztikus és mini-batch változatok általában gyorsabbak és kevésbé hajlamosak lokális minimumokba ragadni, de zajosabbak is.

A gradiens ereszkedés hatékony eszköz a lineáris regressziós modellek optimalizálására, lehetővé téve a pontosabb előrejelzéseket és a jobb modellek létrehozását.

Egyszerű lineáris regresszió vs. többszörös lineáris regresszió

A lineáris regresszió alapvetően a változók közötti kapcsolatot vizsgálja. Két fő típusa létezik: az egyszerű lineáris regresszió és a többszörös lineáris regresszió. A különbség a magyarázó változók számában rejlik.

Az egyszerű lineáris regresszió egyetlen magyarázó (független) változó és egyetlen függő változó közötti lineáris kapcsolatot modellezi. Például, vizsgálhatjuk a hirdetésekre költött összeg hatását az eladásokra. Az egyenlet egyszerűen: y = ax + b, ahol ‘y’ a függő változó, ‘x’ a független változó, ‘a’ a meredekség, és ‘b’ a tengelymetszet.

Ezzel szemben a többszörös lineáris regresszió több magyarázó változót használ a függő változó értékének előrejelzésére. Ez lehetővé teszi, hogy komplexebb kapcsolatokat modellezzünk. Például, az eladásokat befolyásolhatja a hirdetésekre költött összeg, a termék ára és a versenytársak aktivitása is. Ekkor az egyenlet bonyolultabbá válik: y = a₁x₁ + a₂x₂ + … + a_nx_n + b, ahol x₁, x₂, …, x_n a különböző magyarázó változók, és a₁, a₂, …, a_n a hozzájuk tartozó együtthatók.

A többszörös lineáris regresszió pontosabb előrejelzéseket tesz lehetővé, különösen akkor, ha a függő változóra több tényező is hatással van.

A többszörös regresszió használatakor figyelembe kell venni a kollinearitás problémáját, amikor a magyarázó változók között erős korreláció áll fenn. Ez torzíthatja az eredményeket és megnehezítheti az együtthatók értelmezését. A megfelelő változó kiválasztás és a modell validálása kulcsfontosságú a megbízható eredmények eléréséhez.

A determinációs együttható (R-négyzet): A modell jóságának mérése

A lineáris regresszió modelljének teljesítményét számos módon értékelhetjük. Az egyik leggyakrabban használt mérőszám erre a célra a determinációs együttható, közismertebb nevén az R-négyzet (R²).

Az R² azt mutatja meg, hogy a modellünk mennyire jól magyarázza a függő változó varianciáját a független változók segítségével. Más szóval, a modell által megmagyarázott variancia arányát fejezi ki a teljes varianciához képest.

Az R² értéke 0 és 1 között mozog.

• Az R² = 0 azt jelenti, hogy a modellünk egyáltalán nem magyarázza a varianciát, a predikciók nem jobbak, mint egy egyszerű átlagérték használata.
• Az R² = 1 pedig azt jelenti, hogy a modell tökéletesen magyarázza a varianciát, a predikciók pontosan megegyeznek a megfigyelt értékekkel.

Minél közelebb van az R² értéke az 1-hez, annál jobban illeszkedik a modell az adatokra, és annál jobban képes megmagyarázni a függő változó viselkedését.

Ugyanakkor érdemes óvatosnak lenni az R² érték önmagában való értelmezésével. Egy magas R² érték nem feltétlenül jelenti azt, hogy a modellünk „jó”. Például, ha a modellünk túlságosan illeszkedik az adatokra (overfitting), akkor az R² értéke magas lehet, de a modellünk nem fog jól teljesíteni új, eddig nem látott adatokon.

Az korrigált R-négyzet (Adjusted R²) egy javított változata az R²-nek, ami figyelembe veszi a modellben szereplő prediktorok számát. Ezáltal képes kezelni az overfitting problémáját, és megbízhatóbb képet ad a modell valós teljesítményéről, különösen akkor, ha sok prediktort használunk.

Az R²-t mindig a kontextusban kell értelmezni. Egy adott alkalmazásban elfogadható R² érték függ az adatok jellegétől, a kutatási kérdéstől, és a többi elérhető modelltől. Nem létezik „jó” vagy „rossz” R² érték önmagában.

A korrigált R-négyzet (Adjusted R-squared) és annak jelentősége

A korrigált R-négyzet (Adjusted R-squared) a lineáris regressziós modellek teljesítményének értékelésére szolgáló metrika, mely bünteti a modellbe feleslegesen bevont prediktorokat. Az R-négyzet (R-squared) azt mutatja meg, hogy a modellünk mennyire jól magyarázza a függő változó varianciáját. Azonban az R-négyzet értéke szinte mindig nő, ha újabb prediktort adunk a modellhez, még akkor is, ha az a prediktor valójában nem releváns.

A korrigált R-négyzet ezt a problémát orvosolja. Figyelembe veszi a mintaszámot (n) és a prediktorok számát (k) is. Minél több prediktort adunk a modellhez, annál nagyobb lesz a büntetés, és annál kisebb lesz a korrigált R-négyzet értéke, ha a hozzáadott prediktor nem javítja jelentősen a modell illeszkedését.

A korrigált R-négyzet tehát egy objektívebb mérőszám, mint az R-négyzet, különösen akkor, ha több prediktorral dolgozunk.

A korrigált R-négyzet képlete:

Adjusted R² = 1 – [(1-R²)(n-1)/(n-k-1)]

Ahol:

• R² az R-négyzet értéke
• n a minták száma
• k a prediktorok száma

Általánosságban elmondható, hogy a korrigált R-négyzet értéke mindig kisebb vagy egyenlő, mint az R-négyzet. A két érték közötti különbség annál nagyobb, minél több prediktort használunk, és minél kisebb a mintanagyság.

A lineáris regresszió feltételei: Linearitás, függetlenség, homoszkedaszticitás, normalitás

A lineáris regresszió hatékony eszköz, de megbízhatósága nagymértékben függ attól, hogy a mögöttes feltételezések teljesülnek-e. Ezek a feltételezések biztosítják, hogy a modell által szolgáltatott eredmények értelmezhetőek és helytállóak legyenek. Négy alapvető feltétel létezik:

• Linearitás: A független és függő változók közötti kapcsolatnak lineárisnak kell lennie. Ez azt jelenti, hogy a független változó változásának hatása a függő változóra állandó. Ha a kapcsolat nem lineáris, a lineáris regresszió pontatlan eredményeket adhat.
• Függetlenség (Independence): Az adatok pontjainak függetlennek kell lenniük egymástól. Ez azt jelenti, hogy egy adatpont értéke nem befolyásolja egy másik adatpont értékét. Például, idősoros adatoknál gyakori probléma az autokorreláció, ami megsérti ezt a feltételt.
• Homoszkedaszticitás: A hibatagok varianciája a független változó minden értékénél azonos kell, hogy legyen. Más szóval, a pontok szóródása a regressziós vonal körül egyenletes kell legyen. Ha a variancia nem egyenletes (heteroszkedaszticitás), a standard hibák pontatlanok lesznek, ami hibás következtetésekhez vezethet.
• Normalitás: A hibatagoknak normális eloszlásúaknak kell lenniük. Ez a feltételezés különösen fontos a statisztikai tesztek és a konfidencia intervallumok megbízhatósága szempontjából.

A lineáris regresszió érvényességének kulcsa a feltételek teljesülése. Amennyiben ezek a feltételek sérülnek, a modell eredményei torzítottak és megbízhatatlanok lehetnek.

A feltételek megsértése esetén különböző módszerekkel lehet korrigálni a modellt. Például, a nem-linearitást transzformációkkal, a heteroszkedaszticitást súlyozott legkisebb négyzetek módszerével, az autokorrelációt pedig idősoros modellekkel lehet kezelni. A hibatagok normalitásának hiánya esetén nem-paraméteres módszerek alkalmazása javasolt.

A lineáris regresszió helyes alkalmazása és a feltételek ellenőrzése elengedhetetlen a megbízható és értelmezhető eredmények eléréséhez. A feltételek megsértésének tudatosítása és a megfelelő korrekciós lépések megtétele biztosítja, hogy a modell a valósághoz közeli képet adjon.

A feltételek megsértésének következményei és orvoslási lehetőségei

A lineáris regresszió alapvető feltételezéseinek megsértése komoly következményekkel járhat a modell pontosságára és megbízhatóságára. A leggyakoribb problémák közé tartozik a linearitás hiánya, a heteroszkedaszticitás, az autokorreláció és a normalitás megsértése.

A linearitás hiánya azt jelenti, hogy a magyarázó és a függő változó közötti kapcsolat nem lineáris. Ennek eredményeként a modell pontatlan előrejelzéseket adhat. Orvoslására használhatók nemlineáris transzformációk (pl. logaritmikus, négyzetes) a magyarázó változókon, vagy polinomiális regresszió alkalmazható.

A heteroszkedaszticitás azt jelenti, hogy a hiba tagjainak varianciája nem konstans. Ez hibás szórásbecslésekhez vezet, ami megbízhatatlan statisztikai következtetéseket eredményez. A heteroszkedaszticitás kezelésére használhatók súlyozott legkisebb négyzetek (WLS) módszere, vagy a változók transzformációja.

Az autokorreláció, azaz a hibatagok közötti korreláció, különösen idősoros adatoknál gyakori probléma. Ez szintén torzítja a szórásbecsléseket és a szignifikancia vizsgálatokat.

Az autokorreláció kezelésére használhatók ARIMA modellek vagy a Cochrane-Orcutt eljárás, melyek figyelembe veszik a hibatagok közötti kapcsolatot.

A normalitás megsértése, azaz a hibatagok nem normális eloszlása, kevésbé kritikus nagy minták esetén a centrális határeloszlás tétele miatt. Kisebb mintáknál azonban problémát okozhat. A normalitás javítására használható a Box-Cox transzformáció, vagy nemparaméteres regressziós módszerek alkalmazhatók.

Túlzott illeszkedés (Overfitting) és alulilleszkedés (Underfitting) a lineáris regresszióban

A lineáris regresszió alkalmazásakor gyakran találkozunk a túlzott illeszkedés (overfitting) és az alulilleszkedés (underfitting) problémájával. Mindkettő rontja a modell prediktív képességét.

Az alulilleszkedés akkor következik be, amikor a modell nem képes megfelelően megragadni a kapcsolatot a bemeneti változók és a célváltozó között. Ez általában azért történik, mert a modell túl egyszerű (pl. egy egyenes vonal próbál leírni egy komplex görbét). Az alulillesztett modell gyenge teljesítményt nyújt mind a tréning adatokon, mind a teszt adatokon.

Ezzel szemben a túlzott illeszkedés azt jelenti, hogy a modell túlságosan a tréning adatokra fókuszál, beleértve a zajt és az anomáliákat is. Ennek eredményeként a modell tökéletesen illeszkedik a tréning adatokra, de rosszul teljesít az új, ismeretlen adatokon. Túlzott illeszkedés esetén a modell komplexebb (pl. magas fokú polinom), mint amire valójában szükség lenne.

A cél egy olyan modell megtalálása, amely jól általánosít, azaz a tréning adatokon tanult mintákat sikeresen alkalmazza az új adatokra is.

A túlzott illeszkedés elkerülésére többféle módszer létezik, mint például a regularizáció (pl. L1 vagy L2 regularizáció), amely bünteti a modell túl nagy súlyait, vagy a keresztvalidáció, amellyel a modell teljesítményét különböző adathalmazokon mérjük.

Az alulilleszkedés problémájának megoldására pedig érdemes komplexebb modellt választani, vagy további releváns bemeneti változókat bevonni a modellbe.

Regularizációs technikák: Ridge regresszió, Lasso regresszió, Elastic Net

A lineáris regresszió során gyakran szembesülünk a túlillesztés problémájával, különösen amikor sok prediktor változónk van. Ennek elkerülésére regularizációs technikákat alkalmazunk, melyek közül a legnépszerűbbek a Ridge regresszió, a Lasso regresszió és az Elastic Net.

A Ridge regresszió (más néven L2 regularizáció) a lineáris regresszió célfüggvényéhez hozzáad egy büntetést, ami a regressziós együtthatók négyzetének összegével arányos. Ez azt jelenti, hogy a modell arra törekszik, hogy minimalizálja a hibát, miközben az együtthatók értékét is alacsonyan tartja. A Ridge regresszió csökkenti az együtthatók nagyságát, de nem szorítja őket nullára. Ezáltal segít stabilizálni a modellt és csökkenteni a varianciát, de a modell nem végez automatikus változó kiválasztást.

Ezzel szemben a Lasso regresszió (L1 regularizáció) az együtthatók abszolút értékének összegével arányos büntetést alkalmaz. A Lasso képes egyes együtthatókat pontosan nullára állítani, ami automatikus változó kiválasztáshoz vezet. Ez különösen hasznos lehet, ha sok prediktor változónk van, és csak egy részük releváns a célváltozó szempontjából.

A Lasso regresszió előnye, hogy egyszerűsíti a modellt a kevésbé fontos változók eltávolításával, ami javíthatja a modell értelmezhetőségét és általánosítási képességét.

Az Elastic Net egy hibrid megközelítés, amely kombinálja a Ridge és a Lasso regresszió előnyeit. Az Elastic Net célfüggvénye mind az L1, mind az L2 regularizációs tagokat tartalmazza, egy súlyozó paraméterrel (α) szabályozva, hogy melyik regularizációs módszer domináljon. Ha α = 0, akkor az Elastic Net Ridge regresszióvá válik, míg ha α = 1, akkor Lasso regresszióvá.

Az Elastic Net különösen hasznos akkor, ha erősen korrelált prediktor változóink vannak. A Lasso ilyenkor hajlamos csak az egyiket kiválasztani közülük, míg az Elastic Net mindkettőt megtarthatja, de kisebb súllyal. Ezáltal az Elastic Net egy robusztusabb és stabilabb modellt eredményezhet.

A regularizációs technikák alkalmazása során a regularizációs paraméter (λ a Ridge és Lasso esetén, illetve α és λ az Elastic Net esetén) helyes megválasztása kritikus fontosságú. Ezt gyakran keresztvalidációs eljárásokkal határozzuk meg, hogy a modell a lehető legjobban teljesítsen az új adatokon.

A feature engineering szerepe a lineáris regresszió pontosságának növelésében

A lineáris regresszió teljesítménye nagymértékben függ a bemeneti adatok minőségétől és relevanciájától. Itt jön képbe a feature engineering, az a folyamat, melynek során meglévő adatokból új, relevánsabb jellemzőket hozunk létre.

A feature engineering célja, hogy olyan új változókat generáljunk, melyek jobban reprezentálják a modell által leírni kívánt összefüggéseket. Ez történhet a meglévő jellemzők átalakításával (pl. logaritmikus transzformáció, négyzetre emelés), kombinálásával (pl. interakciós változók létrehozása), vagy éppen külső adatok beépítésével.

A jól megtervezett jellemzők jelentősen növelhetik a lineáris regresszió pontosságát, akár akkor is, ha a modell maga egyszerű marad.

Például, ha a modellünk egy termék árát próbálja megjósolni, és tudjuk, hogy az ár és a kereslet között nem lineáris összefüggés van, akkor a kereslet négyzetét is bevonhatjuk jellemzőként. Egy másik példa, ha földrajzi adataink vannak, ahelyett, hogy csak a koordinátákat használnánk, létrehozhatunk jellemzőket, melyek a legközelebbi bevásárlóközpont távolságát jelzik. A polinomiális regresszió is egyfajta feature engineering, ahol a bemeneti változókat magasabb hatványra emeljük.

A feature engineering során azonban figyelni kell a túlzott illeszkedés (overfitting) veszélyére. Ha túl sok, vagy zajos jellemzőt adunk hozzá a modellhez, az a tanító adatokon jól teljesíthet, de új adatokon gyengén fog szerepelni. Ezért fontos a jellemzők kiválasztása, és a modellek validálása, hogy biztosítsuk a jó általánosítást.

Röviden, a feature engineering kulcsfontosságú a lineáris regressziós modellek hatékonyságának maximalizálásában. Az adatok mélyebb megértése és a megfelelő jellemzők létrehozása jelentősen javíthatja a prediktív képességeket.

Kategorikus változók kezelése a lineáris regresszióban: Dummy változók

A lineáris regresszió során gyakran találkozunk kategorikus változókkal, melyek nem numerikus értékeket (pl. szín, nem, régió) vesznek fel. Ezeket közvetlenül nem tudjuk beilleszteni a regressziós modellbe. A megoldás a dummy változók használata.

A dummy változó egy bináris (0 vagy 1) változó, mely egy adott kategória jelenlétét vagy hiányát jelzi. Például, ha a ‘nem’ változó lehetséges értékei ‘férfi’ és ‘nő’, akkor létrehozhatunk egy ‘férfi’ dummy változót. Ha egy megfigyelésnél a nem ‘férfi’, akkor ennek a dummy változónak az értéke 1, egyébként 0.

A lineáris regresszió kategorikus változókkal történő használatához minden kategóriát dummy változóvá kell alakítani, kivéve egyet (referencia kategória).

A referencia kategória azért szükséges, mert ha az összes kategóriát dummy változóvá alakítanánk, multikollinearitás lépne fel, ami torzítja a regressziós együtthatókat. A referencia kategória együtthatója a többi kategóriához viszonyított hatást mutatja.

Például, ha egy termék ‘szín’ változója lehet ‘piros’, ‘kék’ vagy ‘zöld’, akkor létrehozunk egy ‘piros’ és egy ‘kék’ dummy változót. A ‘zöld’ lesz a referencia kategória. A ‘piros’ együtthatója azt mutatja, hogy a ‘piros’ termék átlagosan mennyivel tér el a ‘zöld’ terméktől. A ‘kék’ együtthatója pedig a ‘kék’ és a ‘zöld’ közötti különbséget.

A dummy változók helyes használata elengedhetetlen a kategorikus változók pontos beépítéséhez a lineáris regressziós modellekbe.

A lineáris regresszió alkalmazási területei a gyakorlatban

A lineáris regresszió széles körben alkalmazható a gyakorlatban, mivel egyszerű és hatékony módszer a változók közötti kapcsolatok modellezésére. Az egyik leggyakoribb terület a gazdasági előrejelzés. Például, egy cég felhasználhatja a lineáris regressziót a jövőbeli eladások becslésére a múltbeli eladások, a marketing kiadások és a GDP alapján.

A pénzügyi szektorban is elterjedt a használata. Segítségével modellezhetők a részvényárfolyamok, a kamatlábak és más pénzügyi mutatók közötti összefüggések. A kockázatkezelésben is fontos szerepet játszik, ahol a lineáris regresszióval becsülhetők a portfóliók várható hozamai és kockázatai.

A marketingben a lineáris regresszió lehetővé teszi a marketingkampányok hatékonyságának mérését. Ezzel megállapítható, hogy mely marketingcsatornák hozzák a legtöbb bevételt, és optimalizálhatók a marketing kiadások.

Az orvostudományban a lineáris regresszió alkalmazható a betegségek kockázati tényezőinek azonosítására. Például, meg lehet vizsgálni, hogy a dohányzás, a magas vérnyomás és a koleszterinszint hogyan befolyásolja a szívbetegségek kialakulásának kockázatát.

A lineáris regresszió egy erős eszköz az adatok elemzésére és a jövőbeli eredmények előrejelzésére, de fontos figyelembe venni a modell korlátait és a feltételezéseit.

A környezetvédelemben a lineáris regresszióval modellezhetők a környezeti változók közötti kapcsolatok. Például, meg lehet vizsgálni, hogy a légszennyezés hogyan befolyásolja a növényzet növekedését vagy a vízi ökoszisztémák állapotát.

A társadalomtudományokban a lineáris regresszió használható a társadalmi jelenségek elemzésére. Például, meg lehet vizsgálni, hogy az iskolai végzettség hogyan befolyásolja a jövedelmet vagy a bűnözési rátát.

Lineáris regresszió implementálása Pythonban a Scikit-learn segítségével

A lineáris regresszió Pythonban a Scikit-learn könyvtár segítségével egyszerűen implementálható. A könyvtár egy LinearRegression osztályt kínál, amely a legkisebb négyzetek módszerével illeszti a lineáris modellt az adatokhoz.

Az implementáció első lépése az adatok előkészítése. Ez magában foglalja a bemeneti változók (X) és a célváltozó (y) azonosítását, valamint az adatok megfelelő formátumba alakítását. A Scikit-learn elvárja, hogy X egy kétdimenziós tömb legyen, ahol a sorok a mintákat, az oszlopok pedig a bemeneti változókat reprezentálják. y egy egydimenziós tömbként adható meg.

A modell létrehozása a LinearRegression osztály egy példányának létrehozásával történik: model = LinearRegression(). Ezt követően a fit() metódussal illesztjük a modellt az adatokhoz: model.fit(X, y). A fit() metódus megtanulja a lineáris regresszió együtthatóit, amelyek minimalizálják a négyzetes hibát.

A tanult együtthatók (a regressziós egyenes meredeksége és tengelymetszete) a coef_ és intercept_ attribútumokban érhetők el.

Az illesztett modell segítségével előrejelzéseket készíthetünk új adatokra a predict() metódussal: y_pred = model.predict(X_new). A predict() metódus a tanult együtthatók alapján számítja ki a célváltozó becsült értékeit.

A modell teljesítményének értékelésére különböző metrikák használhatók, mint például a Mean Squared Error (MSE), a Root Mean Squared Error (RMSE) és az R-négyzet. Ezek a metrikák a Scikit-learn metrics moduljában találhatók.

Példa:

• from sklearn.linear_model import LinearRegression
• from sklearn.metrics import mean_squared_error
• model = LinearRegression()
• model.fit(X_train, y_train)
• y_pred = model.predict(X_test)
• mse = mean_squared_error(y_test, y_pred)

A Scikit-learn lineáris regressziós implementációja számos paraméterrel rendelkezik, amelyekkel finomhangolhatjuk a modellt. Ezek a paraméterek lehetővé teszik például a regularizáció alkalmazását, amely segít megelőzni a túltanulást.

A modell kiértékelése: Hibamutatók (MAE, MSE, RMSE)

A lineáris regressziós modell teljesítményének kiértékelése kulcsfontosságú lépés a modell használhatóságának megítélésében. Ebben a folyamatban a hibamutatók játszanak központi szerepet. Ezek a mutatók számszerűen fejezik ki, hogy a modell mennyire pontosan képes előre jelezni a valós értékeket.

Három gyakran használt hibamutató a MAE (Mean Absolute Error), a MSE (Mean Squared Error) és az RMSE (Root Mean Squared Error). A MAE az előrejelzett és a valós értékek közötti különbségek abszolút értékének átlaga. Ez a mutató könnyen értelmezhető, mivel közvetlenül megmutatja, hogy átlagosan mennyivel téved a modell.

A MSE a különbségek négyzetének átlaga. A négyzetre emelés miatt a nagyobb hibákat jobban súlyozza, így érzékenyebb a kiugró értékekre.

Az RMSE a MSE négyzetgyöke. Előnye, hogy a hibát az eredeti mértékegységben adja meg, ami megkönnyíti az értelmezést. Például, ha a célváltozó árakat reprezentál forintban, akkor az RMSE azt mutatja meg, hogy átlagosan hány forinttal tér el a modell előrejelzése a valós ártól.

Mindhárom mutató alacsonyabb értéke jobb modell teljesítményt jelez. Azonban a mutatók konkrét értékeinek értelmezése kontextusfüggő, és függ a vizsgált adatok jellemzőitől és a célkitűzésektől. Fontos, hogy a hibamutatókat együtt értékeljük, és figyelembe vegyük a modell alkalmazási területét is.

A reziduális analízis (Residual Analysis) szerepe a modell diagnosztizálásában

A lineáris regressziós modell diagnosztizálásának kulcsfontosságú eleme a reziduális analízis. A reziduálisok a megfigyelt értékek és a modell által előrejelzett értékek közötti különbségek. Ezek elemzése feltárja, hogy a modell mennyire jól illeszkedik az adatokhoz, és segít azonosítani a modell feltételezéseinek megsértését.

Ideális esetben a reziduálisok véletlenszerűen szóródnak a nulla körül, ami azt jelzi, hogy a modell megfelelően magyarázza a varianciát. Szisztematikus mintázatok a reziduálisokban (pl. görbület, tölcsér alak) arra utalhatnak, hogy a lineáris feltételezés nem érvényes, vagy hogy hiányzó változók vannak a modellben.

A reziduálisok eloszlásának vizsgálata elengedhetetlen a modell érvényességének megítéléséhez.

A reziduálisok szórásának homogenitását is ellenőrizni kell. A heteroszkedaszticitás, azaz a reziduálisok szórásának változása a prediktált értékek függvényében, a modell megbízhatóságát veszélyeztetheti. Ezt gyakran a reziduálisok szórásdiagramján lehet észlelni.

A normális eloszlású reziduálisok feltételezése is fontos, különösen a szignifikancia tesztek és konfidencia intervallumok helyességéhez. Ezt Q-Q diagramokkal vagy hisztogramokkal ellenőrizhetjük. A nagy eltérések a normális eloszlástól a modell problémáira utalhatnak.

Végül, a kiugró értékek azonosítása a reziduálisok segítségével kritikus. A nagy reziduálisok kiugró értékeket jeleznek, amelyek túlzottan befolyásolhatják a modell paramétereit. Ezeket az értékeket alaposan meg kell vizsgálni, és szükség esetén kezelni kell.

A lineáris regresszió kiterjesztései: Polinom regresszió

A lineáris regresszió egyenes vonal illesztésére törekszik az adatokra. A valóságban azonban az összefüggések gyakran nem lineárisak. Ekkor jön képbe a polinom regresszió, mely a lineáris regresszió egy kiterjesztése.

A polinom regresszió lényege, hogy a magyarázó változó (x) magasabb hatványait is bevonjuk a modellbe. Például, egy másodfokú (kvadratikus) polinom regressziós modell a következőképpen néz ki: y = β₀ + β₁x + β₂x², ahol β₀, β₁ és β₂ a modell paraméterei.

A polinom regresszió lehetővé teszi ívelt görbék illesztését az adatokra, így képes megragadni a nem lineáris összefüggéseket.

A polinom fokszámának megválasztása kritikus. Túl alacsony fokszám esetén a modell nem illeszkedik megfelelően az adatokra (alulillesztés). Túl magas fokszám esetén pedig a modell túlságosan illeszkedik az adatokra, és zajt is megtanul, ami rossz általánosításhoz vezet (túlillesztés). A modell komplexitását szabályozni kell.

A polinom regresszió használatakor érdemes figyelni a multikollinearitásra, mivel a magasabb hatványok erősen korrelálhatnak egymással. Ezt a problémát regularizációs technikákkal, például ridge regresszióval lehet kezelni.

Lineáris regresszió vs. más regressziós modellek (pl. logisztikus regresszió)

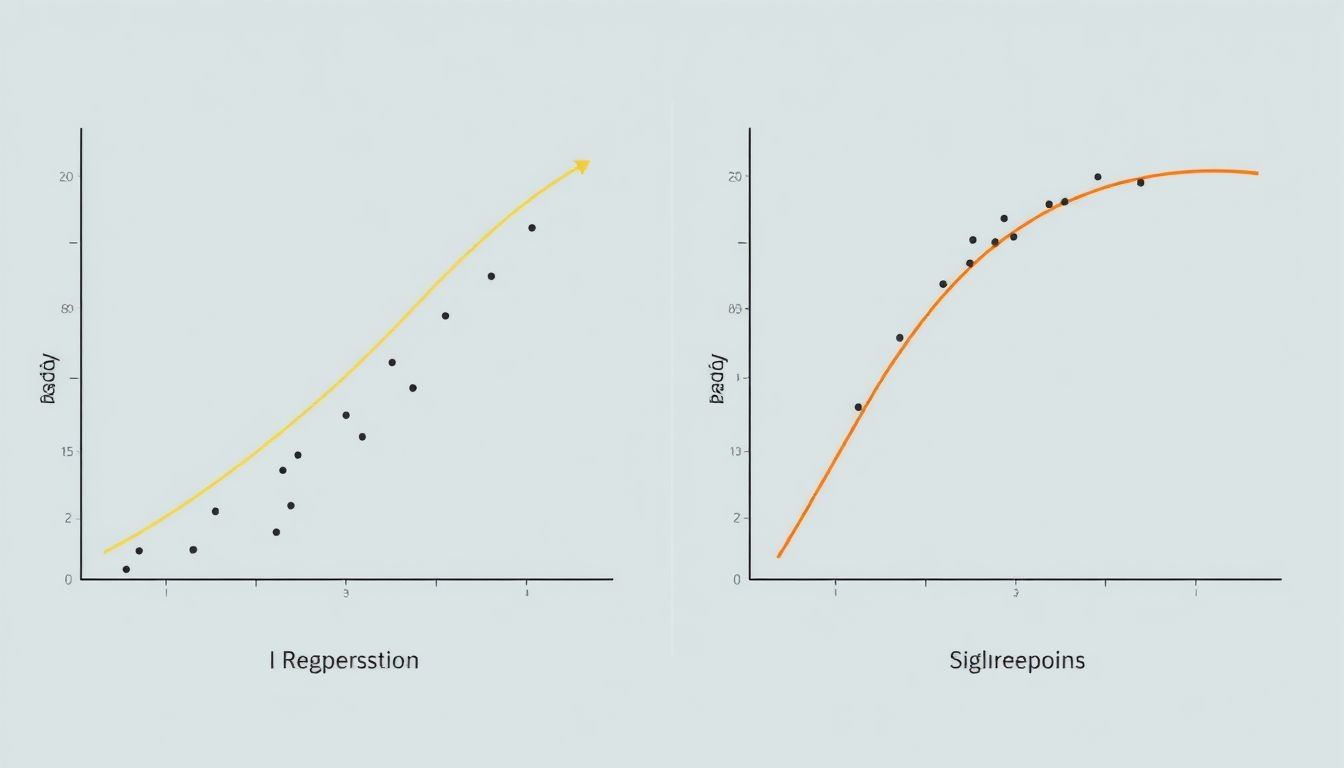
A lineáris regresszió egy folytonos változó értékét igyekszik előre jelezni egy vagy több magyarázó változó alapján. Ezzel szemben, a logisztikus regresszió egy kategorikus (általában bináris) változó valószínűségét becsüli meg.

A lineáris regresszió feltételezi, hogy a magyarázó és a célváltozó között lineáris kapcsolat van, míg a logisztikus regresszió egy szigmoid (S alakú) függvényt használ a valószínűség becslésére, így nem lineáris kapcsolatokat is képes modellezni.

A kimenet szempontjából is jelentős a különbség. A lineáris regresszió egy folytonos értéket ad, míg a logisztikus regresszió egy 0 és 1 közötti valószínűséget, amely alapján eldönthető, hogy egy adott eset melyik kategóriába tartozik.

A lineáris regresszió ideális, ha egy érték nagyságát akarjuk megbecsülni, míg a logisztikus regresszió akkor alkalmazható, ha egy esemény bekövetkezésének valószínűségét szeretnénk meghatározni.

Például, a ház árának előrejelzésére a lineáris regresszió alkalmas, míg annak megjóslására, hogy egy ügyfél hitelképes-e, a logisztikus regresszió a megfelelő választás.

Míg a lineáris regresszió a legkisebb négyzetek módszerét használja a modell paramétereinek becslésére, a logisztikus regresszió az maximum likelihood becslést alkalmazza.