A modern technológia alapjait képező elektromos áram működésének megértéséhez elengedhetetlen a villamos ellenállás fogalmának mélyreható ismerete. Ez a fizikai mennyiség alapvetően meghatározza, hogy egy adott anyag vagy áramköri elem mennyire akadályozza az elektronok áramlását, azaz a villamos áramot. Képzeljünk el egy vízvezetéket: minél szűkebb vagy hosszabb a cső, annál nagyobb az ellenállása a víz áramlásával szemben. Hasonlóképpen, az elektronoknak is „át kell préselődniük” az anyagon, és ez a folyamat nem mindig zökkenőmentes.
Az elektromos ellenállás az anyag belső tulajdonságaiból és a külső tényezőkből adódik. Minden anyag, legyen az vezető vagy szigetelő, rendelkezik valamekkora ellenállással. A különbség csupán nagyságrendi: a vezetők ellenállása rendkívül alacsony, míg a szigetelőké rendkívül magas. Ez a különbség teszi lehetővé, hogy az elektronikus áramkörök precízen működjenek, és az áramot a kívánt úton tereljék.
Az elektromos ellenállás definíciója és alapjai
Az elektromos ellenállás (jelölése: R) az a fizikai mennyiség, amely megmutatja, hogy egy vezető mennyire akadályozza az elektromos áram áthaladását. Más szóval, az ellenállás az a mérték, amennyire egy anyag vagy eszköz ellenáll az elektronok mozgásának, amikor feszültséget alkalmazunk rá. Amikor az elektronok áthaladnak egy vezető anyagon, ütköznek az atomokkal és ionokkal, energiájuk egy része hővé alakul, ami az ellenállás jelenségét okozza.
Ez az ütközés és energiaátadás az oka annak, hogy az ellenálláson áthaladó áram hőtermeléssel jár, amit Joule-hőnek nevezünk. Ez a jelenség hasznos lehet fűtőberendezésekben, de káros is lehet elektronikai eszközökben, ahol a túlmelegedés meghibásodáshoz vezethet. Az ellenállás tehát nem csupán passzív akadály, hanem aktív szerepet játszik az energiaátalakításban is.
Az ellenállás mértékegysége az ohm, amelyet a görög nagy omega (Ω) betűvel jelölünk. Az elnevezés Georg Simon Ohm német fizikustól származik, aki az elektromos áram, a feszültség és az ellenállás közötti alapvető összefüggést, az Ohm törvényét fedezte fel.
Az elektromos ellenállás lényegében az anyag „makacsságát” fejezi ki az elektronok mozgásával szemben, a feszültség és az áram arányában.
Az ellenállás fogalma alapvető fontosságú az elektronika és az elektrotechnika szinte minden területén. Nélküle nem értenénk meg, hogyan működnek az egyszerű áramkörök, a bonyolult számítógépes rendszerek, vagy akár az elektromos hálózatok. Az ellenállás kontrollált alkalmazása lehetővé teszi a mérnökök számára, hogy szabályozzák az áramot és a feszültséget, stabilizálják az áramköröket és védjék az alkatrészeket a túláramtól.
Ohm törvénye: az ellenállás matematikai alapja
Az Ohm törvénye az elektromos ellenállás megértésének sarokköve. Ez az empirikus törvény írja le a feszültség, az áram és az ellenállás közötti alapvető kapcsolatot egy adott áramkörben. Georg Simon Ohm fedezte fel a 19. század elején, és azóta is az elektrotechnika egyik legfontosabb alapelve.
Az Ohm törvénye a következőképpen fogalmazható meg: egy vezetőn átfolyó elektromos áram (I) egyenesen arányos a vezető két végpontja közötti feszültséggel (U) és fordítottan arányos a vezető ellenállásával (R). Matematikailag ez a következőképpen írható fel:
U = I ⋅ R
ahol:
- U a feszültség voltban (V)
- I az áram erőssége amperben (A)
- R az ellenállás ohmban (Ω)
Ezt az egyenletet átalakítva könnyen kiszámítható az áram vagy az ellenállás is, ha a másik két érték ismert:
- I = U / R (Az áram egyenesen arányos a feszültséggel és fordítottan arányos az ellenállással.)
- R = U / I (Az ellenállás a feszültség és az áram hányadosa.)
Ez a három forma rendkívül hasznos az áramkörök elemzésében és tervezésében. Például, ha tudjuk egy ellenállás értékét és a rá eső feszültséget, könnyen kiszámíthatjuk, mennyi áram fog átfolyni rajta. Fordítva, ha egy adott áramot szeretnénk korlátozni egy áramkörben, az Ohm törvénye segítségével meghatározhatjuk a szükséges ellenállás értékét.
Fontos megjegyezni, hogy az Ohm törvénye ideális esetben érvényes, azaz olyan anyagokra, amelyeknek az ellenállása állandó a feszültség és az áram széles tartományában (ezeket ohmos ellenállásoknak nevezzük). Bizonyos anyagok, például a félvezetők diódái vagy tranzisztorai, nem viselkednek ohmikusan, azaz ellenállásuk változik a rájuk kapcsolt feszültség függvényében. Ezekre az anyagokra az Ohm törvénye közvetlenül nem alkalmazható, de az ellenállás fogalma továbbra is releváns a munkapontjuk leírásában.
Az Ohm törvénye nem csak egy matematikai formula, hanem egy mélyreható fizikai elv, amely segít megérteni az energia áramlását és átalakulását az elektromos áramkörökben. Az áramkörök elemzésekor az ellenállás, a feszültség és az áram közötti kölcsönhatás megértése kulcsfontosságú a hibakereséshez, a teljesítményoptimalizáláshoz és az új elektronikai megoldások fejlesztéséhez.
Az ellenállást befolyásoló tényezők
Az elektromos ellenállás nem csupán egy fix érték, hanem számos tényező befolyásolja, amelyek mind az anyag belső szerkezetéből, mind a külső körülményekből adódnak. Ezeknek a tényezőknek az ismerete elengedhetetlen a vezetékek és ellenállások tervezésénél, kiválasztásánál és az áramkörök működésének megértésénél.
Anyagminőség és fajlagos ellenállás
Az anyagminőség talán a legfontosabb tényező, amely befolyásolja az ellenállást. Különböző anyagok eltérő mértékben vezetik az elektromos áramot. Ezt a tulajdonságot a fajlagos ellenállás (ρ, ejtsd: ró) fejezi ki, amely egy anyagra jellemző állandó érték. A fajlagos ellenállás az a mérték, amennyire egy anyagra jellemző, hogy ellenáll az áram áramlásának, függetlenül a méretétől és alakjától.
Minél alacsonyabb egy anyag fajlagos ellenállása, annál jobb vezető. Például az ezüstnek van a legalacsonyabb fajlagos ellenállása, ezért a legjobb vezető, de magas ára miatt ritkán használják széles körben. A réz és az alumínium a leggyakrabban használt vezetők, mivel viszonylag alacsony a fajlagos ellenállásuk és megfizethetőek.
A fajlagos ellenállás mértékegysége az ohm méter (Ωm). Néhány példa a különböző anyagok fajlagos ellenállására szobahőmérsékleten:
| Anyag | Fajlagos ellenállás (Ωm) | Kategória |
|---|---|---|
| Ezüst | 1.59 × 10-8 | Vezető |
| Réz | 1.68 × 10-8 | Vezető |
| Arany | 2.44 × 10-8 | Vezető |
| Alumínium | 2.82 × 10-8 | Vezető |
| Vas | 10 × 10-8 | Vezető |
| Szilícium (tiszta) | 2.3 × 103 | Félvezető |
| Üveg | 1010 – 1014 | Szigetelő |
| Gumi | 1013 – 1015 | Szigetelő |
Ez a táblázat jól mutatja a hatalmas különbségeket a vezetők, félvezetők és szigetelők fajlagos ellenállása között. A félvezetők, mint a szilícium, speciális tulajdonságokkal rendelkeznek: ellenállásuk a szennyezőanyagoktól és a hőmérséklettől függően jelentősen változhat, ami alapvető fontosságú a modern elektronikában.
A vezető hossza
Egy vezető ellenállása egyenesen arányos a hosszával (L). Minél hosszabb egy vezeték, annál több akadályba ütköznek az elektronok az úton, és annál nagyobb az ellenállás. Ez intuitívan is érthető: ha egy hosszú folyosón kell átjutnunk, több időbe és energiába telik, mint egy rövid folyosón. Elektromos szempontból ez azt jelenti, hogy több energia vész el hő formájában, és nagyobb feszültségesés keletkezik a vezetőn.
Ezért van az, hogy a távvezetékek tervezésénél figyelembe kell venni a vezeték hosszát, és vastagabb, jobb vezető anyagokat kell használni a veszteségek minimalizálása érdekében. Hosszú vezetékek esetén még a legjobb vezetők is jelentős ellenállással rendelkezhetnek, ami befolyásolhatja az áramkör teljesítményét, különösen alacsony feszültségű, nagy áramerősségű alkalmazásokban.
A vezető keresztmetszete
A vezető ellenállása fordítottan arányos a keresztmetszetével (A). Minél vastagabb egy vezeték, annál nagyobb „út” áll rendelkezésre az elektronok számára, így könnyebben áramolhatnak. Képzeljük el újra a vízvezetéket: egy szélesebb csőn könnyebben és gyorsabban áramlik a víz, mint egy szűkön. Ugyanez igaz az elektronokra is.
A nagyobb keresztmetszet tehát csökkenti az ellenállást, ami különösen fontos a nagy áramerősségű alkalmazásokban, ahol a túlmelegedés kockázata magas. Például egy háztartás elektromos hálózatában a fővezetékek sokkal vastagabbak, mint egy lámpa vezetékének szálai, hogy biztonságosan elvezessék a nagy áramot anélkül, hogy túlzottan felmelegednének.
Hőmérséklet
A hőmérséklet szintén jelentős hatással van az anyagok ellenállására. A legtöbb vezető anyag, például a fémek, ellenállása növekszik a hőmérséklet emelkedésével. Ennek oka, hogy magasabb hőmérsékleten az atomok és ionok intenzívebben rezegnek a kristályrácsban, ami növeli az elektronokkal való ütközések számát és gyakoriságát, ezáltal akadályozva azok szabad mozgását.
Ezt a jelenséget a hőmérsékleti együttható írja le. A fémek pozitív hőmérsékleti együtthatóval rendelkeznek. Vannak azonban olyan anyagok, mint például a félvezetők, amelyek ellenállása csökken a hőmérséklet emelkedésével (negatív hőmérsékleti együttható). Ennek oka, hogy a hőenergia extra szabad elektronokat generál, amelyek hozzájárulnak az áramvezetéshez. Bizonyos speciális ötvözetek, mint például a konstansán vagy a nikróm, ellenállása alig változik a hőmérséklettel, ami ideálissá teszi őket precíziós ellenállásokhoz vagy fűtőelemekhez.
A hőmérsékletfüggés egy másik fontos alkalmazása a hőmérséklet-érzékelőkben, például a termisztorokban (NTC vagy PTC típusúak). Ezek az ellenállások a hőmérséklet változását ellenállásváltozássá alakítják, amelyet aztán elektromos jelekké lehet konvertálni, lehetővé téve a hőmérséklet mérését és szabályozását.
A fajlagos ellenállás képlete
A fent említett tényezőket összefoglalva, egy vezető ellenállása a következő képlettel számítható ki:
R = ρ ⋅ (L / A)
ahol:
- R az ellenállás ohmban (Ω)
- ρ a fajlagos ellenállás ohm méterben (Ωm)
- L a vezető hossza méterben (m)
- A a vezető keresztmetszete négyzetméterben (m2)
Ez a képlet alapvető fontosságú a vezetékek és ellenállások méretezésénél, valamint az elektromos áramkörök tervezésénél. Segít a mérnököknek optimalizálni az anyagfelhasználást, minimalizálni az energiaveszteségeket és biztosítani az áramkörök biztonságos és hatékony működését.
Az ellenállás mértékegységei és nagyságrendjei
Mint már említettük, az elektromos ellenállás alapvető mértékegysége az ohm (Ω), Georg Simon Ohm tiszteletére. Egy ohm ellenállás az, amelyen 1 volt feszültség hatására 1 amper áram folyik át.
1 Ω = 1 V / 1 A
A gyakorlatban azonban az ellenállás értékek rendkívül széles skálán mozoghatnak, a milliohmoktól (mΩ) egészen a gigaohmokig (GΩ). Éppen ezért gyakran használunk prefixumokat az ohm elnevezés előtt, hogy egyszerűsítsük a nagy vagy kis számok kifejezését:
- Milliohm (mΩ): 1 mΩ = 10-3 Ω (0.001 Ω). Nagyon alacsony ellenállások jelölésére szolgál, például vastag vezetékek, buszvezetékek vagy alacsony ellenállású shunt ellenállások esetében.
- Kilohm (kΩ): 1 kΩ = 103 Ω (1000 Ω). Gyakori érték a legtöbb elektronikai áramkörben, például jelkondicionálásra, feszültségosztásra.
- Megaohm (MΩ): 1 MΩ = 106 Ω (1 000 000 Ω). Magas ellenállások jelölésére szolgál, például bemeneti impedanciákban, szigetelési ellenállásokban.
- Gigaohm (GΩ): 1 GΩ = 109 Ω (1 000 000 000 Ω). Rendkívül magas ellenállások, például szigetelőanyagok ellenállásának mérésére.
Ezek a prefixumok segítenek abban, hogy a mérnökök és technikusok könnyebben kommunikáljanak az ellenállás értékekről anélkül, hogy hosszú sorozatú nullákat kellene leírniuk. Például egy 4700 ohmos ellenállást általában 4.7 kΩ-ként jelölnek.
A különböző nagyságrendű ellenállások mindegyike kulcsfontosságú szerepet játszik az elektronika különböző területein. Az alacsony ellenállások biztosítják az energia hatékony átvitelét, míg a magas ellenállások lehetővé teszik a kis áramok szabályozását vagy a jelek elválasztását. A megfelelő ellenállás kiválasztása kritikus a tervezett áramköri funkciók eléréséhez és a megbízható működéshez.
Az ellenállások típusai és felépítésük
Az ellenállások az elektronikai áramkörök egyik leggyakoribb és legalapvetőbb passzív alkatrészei. Különböző típusokban és kivitelekben léteznek, attól függően, hogy milyen alkalmazásra szánják őket. A főbb kategóriák a fix, változó és speciális ellenállások.
Fix ellenállások
A fix ellenállások olyan alkatrészek, amelyeknek az ellenállás értéke állandó, és a gyártás során rögzítették. Ezek a legelterjedtebb típusok, és számos alkatrészből álló elektronikai eszközben megtalálhatók. Főbb típusaik:
- Szénréteg ellenállások: Ezek a legolcsóbb és leggyakoribb ellenállások. Kerámia hengerre felvitt szénrétegből készülnek. Az ellenállás értékét a szénréteg vastagsága és a spirális vágás mintázata határozza meg. Jellemzőjük a viszonylag nagy tolerancia (5-10%) és a jó frekvenciaválasz.
- Fémréteg ellenállások: Hasonlóan a szénréteg ellenállásokhoz, de a szén helyett fémötvözet réteget (pl. nikkel-króm) visznek fel a kerámia testre. Ezek pontosabbak (1-5% tolerancia) és stabilabbak a hőmérséklet-változásokkal szemben, mint a szénréteg típusok. Gyakran használják precíziós alkalmazásokban.
- Huzalellenállások: Ezek egy szigetelő magra tekercselt ellenálláshuzalból (pl. nikróm) állnak. Nagyobb teljesítményű alkalmazásokhoz tervezték őket, mivel képesek eloszlatni a jelentős Joule-hőt. Az ellenállás értéke a huzal anyagától, hosszától és vastagságától függ. Toleranciájuk általában 1-5% közötti. Hátrányuk, hogy induktív tulajdonságokkal rendelkezhetnek a tekercselt szerkezet miatt, ami magas frekvenciás áramkörökben problémát okozhat.
- Fémoxid ellenállások: Speciális fémoxid anyagokból készülnek, amelyek magas hőmérsékleten stabilabbak, mint a fémréteg ellenállások. Gyakran használják nagyfeszültségű vagy impulzusterhelésű áramkörökben.
- Felületszerelt (SMD) ellenállások: A modern elektronikában a felületszerelt technológia (SMT) dominál. Az SMD ellenállások apró, téglalap alakú kerámia testek, amelyekre vékony fémréteget visznek fel. Kis méretük, nagy pontosságuk és megbízhatóságuk miatt ideálisak a kompakt, nagy sűrűségű áramkörökhöz.
Változó ellenállások (potenciométerek és reosztátok)
A változó ellenállások olyan alkatrészek, amelyeknek az ellenállás értéke manuálisan vagy automatikusan változtatható. Két fő kategóriájuk van:
- Potenciométerek: Ezek három kivezetéssel rendelkező ellenállások, amelyek egy mozgó érintkezőt (csúszkát) tartalmaznak. Az érintkező helyzetét változtatva a teljes ellenállás egy része leágaztatható. Elsődlegesen feszültségosztóként használják őket, például hangerőszabályzókban, fényerő-szabályzókban vagy pozícióérzékelőkben.
- Reosztátok: Ezek két kivezetéssel rendelkező változó ellenállások, amelyeket az áramkörbe sorosan kötve az átfolyó áram szabályozására használnak. Gyakorlatilag egy potenciométer, amelynek csak az egyik végpontját és a csúszkáját használják. Nagyobb áramerősségek szabályozására alkalmasak, például motorok fordulatszámának állítására vagy fényerő-szabályozásra.
Speciális ellenállások
Számos speciális ellenállás létezik, amelyek különleges környezeti vagy elektromos tulajdonságokra reagálnak:
- Termisztorok (hőfüggő ellenállások):
- NTC (Negative Temperature Coefficient): Ellenállásuk csökken a hőmérséklet emelkedésével. Hőmérséklet-érzékelőként, hőmérséklet-kompenzációra vagy áramkorlátozásra használják bekapcsoláskor.
- PTC (Positive Temperature Coefficient): Ellenállásuk növekszik a hőmérséklet emelkedésével. Túlmelegedés elleni védelemre, biztosítékhelyettesítőként vagy fűtőelemként alkalmazzák.
- Fotóellenállások (LDR – Light Dependent Resistor): Ellenállásuk csökken a rájuk eső fény intenzitásának növekedésével. Fényérzékelőként, alkonykapcsolókban vagy optikai vezérlésekben használják.
- Varisztorok (VDR – Voltage Dependent Resistor): Ellenállásuk csökken a rájuk eső feszültség növekedésével. Túlfeszültség-védelemre, például villámcsapás vagy hálózati ingadozások ellen alkalmazzák.
- Feszültségszabályozó diódák (Zener diódák): Bár diódák, speciális ellenállásként viselkednek a letörési tartományban, ahol a feszültség stabil marad az áram ingadozása ellenére. Feszültségstabilizálásra használják.
- Nyúlásmérő bélyegek: A mechanikai deformáció hatására változik az ellenállásuk. Erő, nyomás, súly vagy alakváltozás mérésére szolgálnak.
Az ellenállások sokfélesége rávilágít arra, hogy milyen sokrétű szerepet töltenek be az elektronikában. A megfelelő típus kiválasztása kulcsfontosságú az áramkör stabilitása, megbízhatósága és a kívánt funkciók elérése szempontjából.
Ellenállások jelölése és értékének leolvasása
Az ellenállások fizikai méretüktől és típusuktól függően különböző módon vannak jelölve, hogy az értékük könnyen azonosítható legyen. A két legelterjedtebb módszer a színkód és a számszöveges jelölés.
Színkódos jelölés
A legtöbb axiális kivezetésű, fix ellenállás (pl. szénréteg, fémréteg) értékét színkódokkal jelölik. Ez egy szabványos rendszer, amelyben színes sávok sorozata található az ellenállás testén. Általában 4 vagy 5 sávot használnak, de léteznek 6 sávos ellenállások is, amelyek a hőmérsékleti együtthatót is jelölik.
A sávok jelentése:
- 1. sáv: Az ellenállás értékének első számjegye.
- 2. sáv: Az ellenállás értékének második számjegye.
- 3. sáv: (4 sávos ellenállásnál) Szorzó. Megmutatja, hány nullát kell írni az első két számjegy után, vagy milyen faktorral kell szorozni.
- 3. sáv: (5 vagy 6 sávos ellenállásnál) Az ellenállás értékének harmadik számjegye.
- 4. sáv: (5 vagy 6 sávos ellenállásnál) Szorzó.
- Utolsó sáv (általában arany vagy ezüst): Tolerancia. Megadja, hogy az ellenállás tényleges értéke mennyire térhet el a névleges értéktől százalékban.
- 6. sáv (ha van): Hőmérsékleti együttható (ppm/°C).
A színek és a hozzájuk tartozó értékek a következők:
| Szín | 1. Számjegy | 2. Számjegy | 3. Számjegy | Szorzó | Tolerancia | Hőmérsékleti együttható (ppm/°C) |
|---|---|---|---|---|---|---|
| Fekete | 0 | 0 | 0 | 100 (×1) | ||
| Barna | 1 | 1 | 1 | 101 (×10) | ±1% | 100 |
| Vörös | 2 | 2 | 2 | 102 (×100) | ±2% | 50 |
| Narancs | 3 | 3 | 3 | 103 (×1k) | 15 | |
| Sárga | 4 | 4 | 4 | 104 (×10k) | 25 | |
| Zöld | 5 | 5 | 5 | 105 (×100k) | ±0.5% | |
| Kék | 6 | 6 | 6 | 106 (×1M) | ±0.25% | 10 |
| Ibolya | 7 | 7 | 7 | 107 (×10M) | ±0.1% | 5 |
| Szürke | 8 | 8 | 8 | 108 (×100M) | ||
| Fehér | 9 | 9 | 9 | 109 (×1G) | ||
| Arany | 10-1 (×0.1) | ±5% | ||||
| Ezüst | 10-2 (×0.01) | ±10% | ||||
| Nincs szín | ±20% |
Példa egy 4 sávos ellenállásra: Barna-Fekete-Vörös-Arany
1. sáv (Barna) = 1
2. sáv (Fekete) = 0
3. sáv (Vörös) = ×100
4. sáv (Arany) = ±5%
Ez tehát egy 10 × 100 Ω = 1000 Ω = 1 kΩ-os ellenállás ±5% toleranciával.
Példa egy 5 sávos ellenállásra: Sárga-Ibolya-Fekete-Barna-Vörös
1. sáv (Sárga) = 4
2. sáv (Ibolya) = 7
3. sáv (Fekete) = 0
4. sáv (Barna) = ×10
5. sáv (Vörös) = ±2%
Ez tehát egy 470 × 10 Ω = 4700 Ω = 4.7 kΩ-os ellenállás ±2% toleranciával.
Számszöveges jelölés (SMD ellenállások)
A felületszerelt (SMD) ellenállások, mivel rendkívül kicsik, nem használhatnak színkódokat. Ehelyett általában numerikus vagy alfanumerikus kódokkal vannak jelölve a testükön.
- 3 számjegyes kód: Az első két számjegy az ellenállás értékét adja meg, a harmadik a szorzó (a nullák száma).
- Például: 102 = 10 × 102 = 1000 Ω = 1 kΩ.
- 473 = 47 × 103 = 47000 Ω = 47 kΩ.
- Ha van „R” betű, az tizedesvesszőként funkcionál: 4R7 = 4.7 Ω.
- 4 számjegyes kód: Az első három számjegy az ellenállás értékét adja meg, a negyedik a szorzó.
- Például: 1002 = 100 × 102 = 10000 Ω = 10 kΩ.
- 4701 = 470 × 101 = 4700 Ω = 4.7 kΩ.
- EIA-96 kód: Nagy pontosságú (1%-os) SMD ellenállásokhoz használják. Ez egy két számjegyből álló kód, amelyet egy betű követ. A két számjegy egy táblázatban keresendő értéket jelöl, a betű pedig a szorzót.
- Például: 01A = 100 Ω.
- 51C = 332 × 100 = 33.2 kΩ.
A megfelelő jelölési rendszer ismerete elengedhetetlen az elektronikai alkatrészek pontos azonosításához és a hibamentes áramkörépítéshez.
Az ellenállás mérése
Az elektromos ellenállás pontos mérése alapvető fontosságú az elektronikai hibakeresésben, az áramkörök tesztelésében és az alkatrészek ellenőrzésében. Számos módszer létezik az ellenállás mérésére, a legegyszerűbbtől a rendkívül precízig.
Digitális multiméterrel
A leggyakoribb és legkönnyebben hozzáférhető eszköz az ellenállás mérésére a digitális multiméter. Szinte minden multiméter rendelkezik „ohm” vagy Ω funkcióval. A mérés menete a következő:
- Kapcsoljuk ki az áramot az áramkörben, és válasszuk le az ellenállást, ha lehetséges. Az ellenállást mindig feszültségmentes állapotban kell mérni. Ha az ellenállás be van kötve egy áramkörbe, más alkatrészek párhuzamos ellenállása torzíthatja a mérést.
- Válasszuk ki a multiméteren az ellenállásmérő (ohm) funkciót.
- Csatlakoztassuk a multiméter mérővezetékeit (piros és fekete) az ellenállás két végére. Fontos, hogy a mérővezetékek ne érjenek össze, és ne érintsük meg az ellenállás kivezetéseit puszta kézzel, mert a testünk ellenállása is befolyásolhatja a mérést, különösen nagy ellenállások esetén.
- Olvassuk le az értéket a multiméter kijelzőjéről. A multiméter automatikusan kiválaszthatja a megfelelő mérési tartományt (auto-range), de manuálisan is beállítható, ha ismerjük az ellenállás nagyságrendjét.
A multiméterek egyszerűek és gyorsak, de pontosságuk korlátozott lehet, különösen nagyon alacsony vagy nagyon magas ellenállások esetén. A legtöbb hobbi és otthoni felhasználásra azonban teljesen elegendőek.
Wheatstone-híddal
A Wheatstone-híd egy precíziós mérőáramkör, amelyet nagyon pontos ellenállásmérésekre használnak, különösen akkor, ha a multiméter pontossága nem elegendő. A híd négy ellenállásból áll, amelyek egy négyzet alakban vannak elrendezve. Ezek közül három ismert értékű, egy pedig az ismeretlen ellenállás.
A híd működési elve a következő:
1. A hidat egy feszültségforrás táplálja.
2. Az egyik átlóban egy érzékeny galvanométer (vagy más feszültségmérő) található, amely a híd két pontja közötti feszültségkülönbséget méri.
3. Az ismert ellenállások értékét addig változtatják, amíg a galvanométer nullát nem mutat. Ez az állapot a híd kiegyensúlyozott állapota.
4. Kiegyensúlyozott állapotban a híd két ágának ellenállásainak aránya megegyezik, így az ismeretlen ellenállás értéke pontosan kiszámítható a többi ellenállás értékéből.
A Wheatstone-híd különösen hasznos érzékelők, például nyúlásmérő bélyegek mérésére, ahol az ellenállás apró változásai nagy jelentőséggel bírnak. Bár bonyolultabb, mint a multiméter, sokkal nagyobb pontosságot kínál.
LCR mérővel
Az LCR mérő egy speciális eszköz, amely nem csak az ellenállást (R), hanem az induktivitást (L) és a kapacitást (C) is képes mérni. Ezek az eszközök általában nagyobb pontosságot és szélesebb mérési tartományt kínálnak, mint a hagyományos multiméterek, és képesek az alkatrészek váltakozó áramú (AC) tulajdonságait is vizsgálni, ami különösen fontos az induktivitás és kapacitás mérésénél, de az ellenállás mérésénél is figyelembe vehetők a parazita hatások.
Az ellenállás mérése során mindig ügyeljünk a biztonságra, különösen magas feszültségű áramkörökben. A megfelelő mérési technika és a megfelelő eszköz kiválasztása kulcsfontosságú a pontos és megbízható eredmények eléréséhez.
Ellenállások soros és párhuzamos kapcsolása
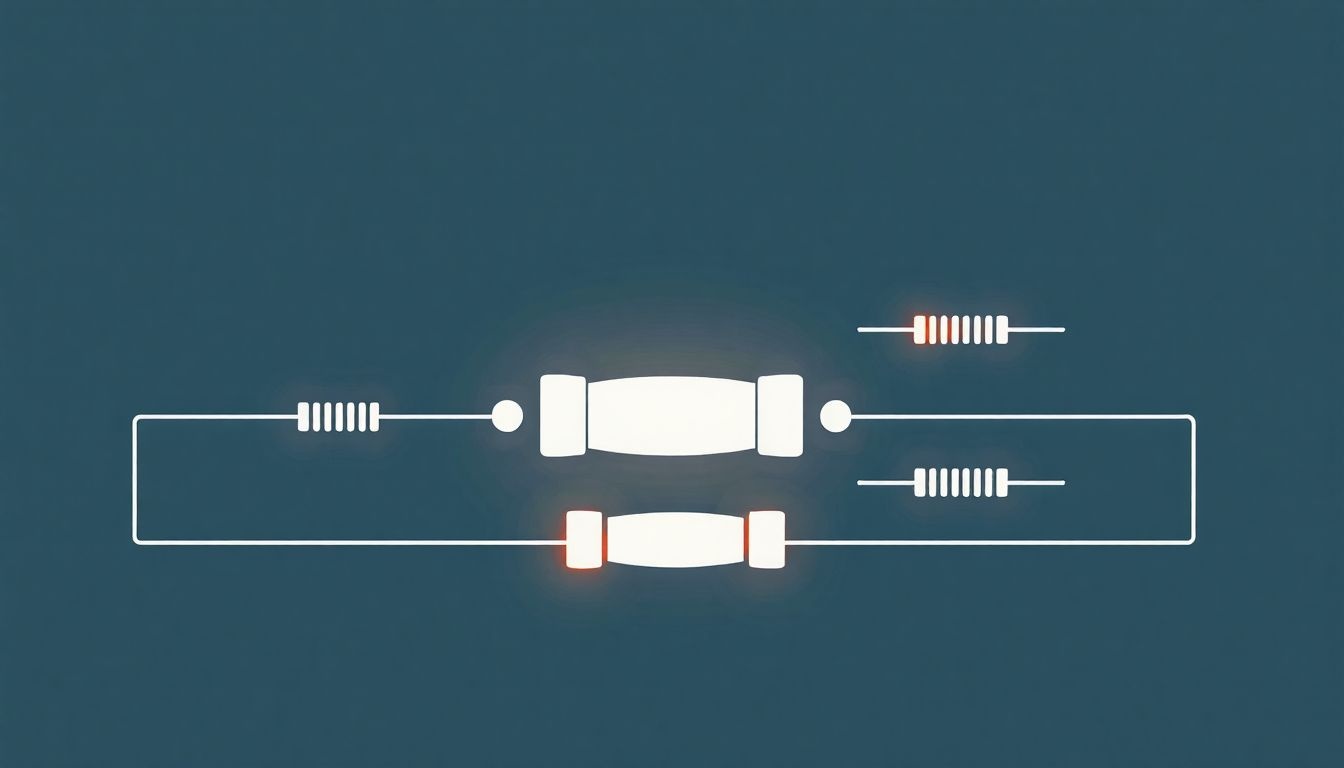
Az elektromos áramkörök tervezésénél és elemzésénél gyakran előfordul, hogy több ellenállást kapcsolunk össze. Az ellenállások kapcsolása alapvetően kétféle lehet: soros és párhuzamos. Mindkét kapcsolási mód eltérő módon befolyásolja az áramkör teljes ellenállását (ekvivalens ellenállását), az árameloszlást és a feszültségesést.
Soros kapcsolás
Két vagy több ellenállás akkor van sorosan kapcsolva, ha egymás után, egyetlen áramútban helyezkednek el, úgy, hogy az egyik ellenállás kivezetése a következő ellenállás kivezetéséhez csatlakozik, és nincs elágazás közöttük. Ebben az esetben az áram azonos az összes ellenálláson keresztül.
A sorosan kapcsolt ellenállások jellemzői:
- Az áram: Az összes sorosan kapcsolt ellenálláson ugyanaz az áram folyik át (Iteljes = I1 = I2 = I3 = …).
- A feszültség: A teljes feszültség (Uteljes) megoszlik az egyes ellenállások között. Az egyes ellenállásokra eső feszültségek összege adja a teljes feszültséget (Uteljes = U1 + U2 + U3 + …). Ez a feszültségosztó elv alapja.
- Az ekvivalens ellenállás: A sorosan kapcsolt ellenállások eredő vagy ekvivalens ellenállása (Rekv) az egyes ellenállások értékeinek összege.
Rekv = R1 + R2 + R3 + … + Rn
Példa: Ha van egy 10 Ω-os és egy 20 Ω-os ellenállás sorosan kapcsolva, az eredő ellenállás 10 + 20 = 30 Ω lesz. Ez azt jelenti, hogy a két ellenállás helyettesíthető egyetlen 30 Ω-os ellenállással az áramkör szempontjából.
Soros kapcsolás esetén az áramkör teljes ellenállása mindig nagyobb, mint a legnagyobb egyedi ellenállás.
Párhuzamos kapcsolás
Két vagy több ellenállás akkor van párhuzamosan kapcsolva, ha mindegyik ellenállás mindkét végpontja ugyanazokhoz a két csomóponthoz csatlakozik, így az áram több úton is áramolhat. Ebben az esetben az összes párhuzamos ágon ugyanaz a feszültség esik.
A párhuzamosan kapcsolt ellenállások jellemzői:
- A feszültség: Az összes párhuzamosan kapcsolt ellenálláson ugyanaz a feszültség esik (Uteljes = U1 = U2 = U3 = …).
- Az áram: A teljes áram (Iteljes) megoszlik az egyes ellenállások között. Az egyes ágakon átfolyó áramok összege adja a teljes áramot (Iteljes = I1 + I2 + I3 + …). Az áram megoszlása fordítottan arányos az ellenállások értékével: a kisebb ellenálláson több áram folyik át. Ez az áramosztó elv alapja.
- Az ekvivalens ellenállás: A párhuzamosan kapcsolt ellenállások eredő vagy ekvivalens ellenállása (Rekv) a reciprok értékek összegének reciproka.
1 / Rekv = 1 / R1 + 1 / R2 + 1 / R3 + … + 1 / Rn
Két ellenállás speciális esetére a következő egyszerűbb képlet használható:
Rekv = (R1 ⋅ R2) / (R1 + R2)
Példa: Ha van egy 10 Ω-os és egy 20 Ω-os ellenállás párhuzamosan kapcsolva, az eredő ellenállás:
Rekv = (10 × 20) / (10 + 20) = 200 / 30 ≈ 6.67 Ω.
Ez azt jelenti, hogy a két ellenállás helyettesíthető egyetlen 6.67 Ω-os ellenállással az áramkör szempontjából.
Párhuzamos kapcsolás esetén az áramkör teljes ellenállása mindig kisebb, mint a legkisebb egyedi ellenállás.
A soros és párhuzamos kapcsolások megértése alapvető az áramkörök analíziséhez, a kívánt ellenállás értékek létrehozásához standard alkatrészekből, és a feszültség- vagy áramelosztás szabályozásához. Ezek az alapelvek érvényesek mind az egyszerű ellenállás áramkörökre, mind a komplexebb elektronikai rendszerekre.
Teljesítménydisszipáció és Joule-hő
Amikor elektromos áram folyik át egy ellenálláson, az elektronok ütköznek az anyag atomjaival, energiájuk egy része hővé alakul. Ezt a jelenséget Joule-hőnek nevezzük, és az ellenállás egyik legfontosabb következménye. Az ellenállás által elnyelt és hővé alakított energia sebességét a teljesítménydisszipáció fejezi ki.
A Joule-hő jelensége
A Joule-hő, más néven ohmos melegedés vagy ellenállásfűtés, az a folyamat, amely során az elektromos áram által egy vezetőben disszipált energia hő formájában leadódik. James Prescott Joule fedezte fel, hogy a hőtermelés arányos az áram négyzetével és az ellenállással.
A disszipált teljesítmény (P) a következő képlettel számítható ki:
P = I2 ⋅ R
Ahol:
- P a teljesítmény wattban (W)
- I az áram erőssége amperben (A)
- R az ellenállás ohmban (Ω)
Az Ohm törvényét (U = I ⋅ R) felhasználva a képlet két másik formában is kifejezhető:
- P = U ⋅ I
- P = U2 / R
Ezek a képletek alapvetőek a teljesítmény kiszámításához az elektromos áramkörökben. Megmutatják, hogy az ellenállás nem csupán akadályozza az áramot, hanem energiát is átalakít.
Alkalmazások és kihívások
A Joule-hő jelensége kettős természetű: bizonyos esetekben hasznos, máskor pedig problémát jelent.
Hasznos alkalmazások:
- Fűtőberendezések: Az elektromos fűtőtestek, bojlereket, hajszárítók, kenyérpirítók mind a Joule-hő elvén működnek. Az ellenálláshuzal (gyakran nikróm) felmelegszik az áram hatására, és hőt bocsát ki.
- Izzólámpák: Az izzószál (volfrám) ellenállásán átfolyó áram olyan mértékben felhevíti az anyagot, hogy az izzásba jön és fényt bocsát ki.
- Biztosítékok: A biztosítékok egy vékony, nagy ellenállású huzalból állnak. Ha túl nagy áram folyik át rajtuk, a Joule-hő hatására a huzal megolvad és megszakítja az áramkört, megvédve ezzel az érzékenyebb alkatrészeket.
Kihívások és problémák:
- Energiaveszteség: Az elektromos energia egy része mindig hővé alakul a vezetékekben és alkatrészekben az ellenállás miatt. Ez energiaveszteséget jelent, ami csökkenti a rendszerek hatékonyságát.
- Túlmelegedés: Az elektronikai alkatrészek, különösen a félvezetők, érzékenyek a hőmérsékletre. A túlzott Joule-hő károsíthatja az alkatrészeket, csökkentheti élettartamukat vagy akár azonnali meghibásodáshoz is vezethet. Ezért van szükség hűtőbordákra és ventilátorokra a processzorokban, erősítőkben és más nagy teljesítményű eszközökben.
- Teljesítményhatár: Minden ellenállás rendelkezik egy maximális teljesítményhatárral (wattban megadva), amelyet biztonságosan el tud disszipálni anélkül, hogy károsodna. A tervezőknek ezt figyelembe kell venniük az alkatrészek kiválasztásakor.
A teljesítménydisszipáció és a Joule-hő megértése kritikus az áramkörök megbízható és hatékony működésének biztosításához. A mérnököknek egyensúlyt kell találniuk az ellenállás kívánt funkciója és a vele járó hőtermelés között, optimalizálva a hűtést és a teljesítményfelvételt.
Az ellenállás alkalmazásai az elektronikában és a mindennapi életben
Az elektromos ellenállás nem csupán egy elméleti fogalom, hanem az elektronika és az elektrotechnika alapköve, amelynek számos gyakorlati alkalmazása van a mindennapi életünkben. Az ellenállások kontrollált felhasználása teszi lehetővé, hogy az elektronikus eszközök a kívánt módon működjenek.
Áramkorlátozás
Az ellenállások egyik leggyakoribb alkalmazása az áramkorlátozás. Sok elektronikai alkatrész, például a LED-ek, csak meghatározott áramerősséggel működhetnek biztonságosan. Ha túl nagy áram folyna át rajtuk, tönkremennének. Egy megfelelően méretezett soros ellenállás beiktatásával az áramkörbe korlátozható az átfolyó áram, így megvédve az érzékeny alkatrészeket.
Például egy LED-hez, amely jellemzően 20 mA áramot igényel, és egy 5 V-os tápegységhez csatlakozik, az Ohm törvénye alapján kiszámítható a szükséges ellenállás értéke, figyelembe véve a LED nyitófeszültségét (pl. 2V). Ebben az esetben az ellenálláson eső feszültség 5V – 2V = 3V, és R = U/I = 3V / 0.02A = 150 Ω ellenállásra lenne szükség.
Feszültségosztás
A feszültségosztó egy olyan áramkör, amely két vagy több sorosan kapcsolt ellenállásból áll, és amely lehetővé teszi, hogy a teljes bemeneti feszültségből kisebb, szabályozott feszültségeket kapjunk. A kimeneti feszültség az ellenállások arányától függ.
Ukimenet = Ubemenet ⋅ (R2 / (R1 + R2))
A feszültségosztókat széles körben alkalmazzák:
- Szenzorok: Sok érzékelő (pl. fényérzékelő, hőmérséklet-érzékelő) ellenállása változik a környezeti tényezők hatására. Egy feszültségosztóba kötve ez az ellenállásváltozás mérhető feszültségváltozássá alakítható, amelyet aztán egy mikrovezérlő vagy analóg-digitális átalakító feldolgozhat.
- Potenciométerek: A potenciométerek valójában változtatható feszültségosztók, amelyekkel manuálisan állítható a kimeneti feszültség, például hangerőszabályzókban, fényerő-szabályzókban vagy pozícióérzékelőkben.
Időzítő áramkörök (RC áramkörök)
Az ellenállások kondenzátorokkal (C) együtt használva RC időzítő áramköröket alkotnak. Ezek az áramkörök a kondenzátor töltésének és kisülésének idejét szabályozzák az ellenállás értékétől függően. Az időállandó (τ, tau) az ellenállás és a kapacitás szorzata:
τ = R ⋅ C
Ezeket az áramköröket használják:
- Késleltető áramkörök: Meghatározott idő után kapcsolnak be vagy ki egy eszközt.
- Szűrő áramkörök: Aluláteresztő vagy felüláteresztő szűrőket alkotnak, amelyek bizonyos frekvenciákat elengednek, másokat pedig csillapítanak. Ez alapvető fontosságú az audioberendezésekben és a jelfeldolgozásban.
- Oszcillátorok: Bizonyos frekvenciájú jelek generálására használják.
Fűtőelemek
Mint már említettük, az ellenállások hőtermelő tulajdonsága (Joule-hő) hasznosítható fűtőelemekben. Az elektromos fűtőtestek, bojlerek, hajszárítók mind ellenálláshuzalt használnak, amely az áram hatására felmelegszik és hőt bocsát ki. A megfelelő ellenállás kiválasztásával szabályozható a hőtermelés mértéke.
Érzékelők
Számos érzékelő működési elve az ellenállás változásán alapul valamilyen fizikai paraméter (hőmérséklet, fény, nyomás, deformáció) hatására:
- Termisztorok: Hőmérséklet-változásra reagálnak az ellenállásuk változásával. Hőmérsékletmérésre, -szabályozásra és -kompenzációra használják.
- Fotóellenállások (LDR): Fényérzékelők, amelyek ellenállása a fényintenzitással változik. Alkonykapcsolókban, fénymérőkben alkalmazzák.
- Nyúlásmérő bélyegek: Mechanikai deformációra (húzás, nyomás) változtatják ellenállásukat. Erő, súly, nyomás mérésére szolgálnak, például mérlegekben, szenzorokban.
Ezen alkalmazások mindegyike azt mutatja, hogy az elektromos ellenállás nem csupán egy alapvető fizikai jelenség, hanem egy rendkívül sokoldalú eszköz, amely nélkülözhetetlen a modern technológia működéséhez, a legegyszerűbb áramköröktől a legkomplexebb rendszerekig.
Fajlagos ellenállás és vezetőképesség: a különbség megértése
Az elektromos ellenállás fogalmának megértéséhez elengedhetetlen a fajlagos ellenállás (rezisztivitás) és a vezetőképesség (konduktivitás) közötti különbség tisztázása. Bár szorosan összefüggenek, nem felcserélhetők, és különböző szempontból jellemzik az anyagokat.
Fajlagos ellenállás (ρ)
A fajlagos ellenállás (ρ) egy anyagra jellemző belső tulajdonság, amely megmutatja, hogy az anyag mennyire ellenáll az elektromos áram áramlásának. Ez egy intenzív mennyiség, ami azt jelenti, hogy nem függ az anyag alakjától vagy méretétől, csak az anyagi minőségtől és a hőmérséklettől.
Mint korábban említettük, a fajlagos ellenállás mértékegysége az ohm méter (Ωm). Egy anyagnak annál nagyobb a fajlagos ellenállása, minél rosszabb vezető. Például a réz fajlagos ellenállása alacsony, míg az üvegé rendkívül magas.
A fajlagos ellenállás határozza meg, hogy egy adott anyagból készült, meghatározott hosszúságú (L) és keresztmetszetű (A) vezetőnek mekkora lesz az ellenállása (R):
R = ρ ⋅ (L / A)
Ez a képlet rávilágít arra, hogy míg a fajlagos ellenállás az anyag inherent tulajdonsága, az ellenállás egy adott fizikai objektum (pl. egy vezetékdarab, egy ellenállás alkatrész) tulajdonsága, amely függ az anyagától, de a geometriai méreteitől is.
Vezetőképesség (σ)
A vezetőképesség (σ, szigma) a fajlagos ellenállás reciprok értéke. Ez az a fizikai mennyiség, amely megmutatja, hogy egy anyag mennyire jól vezeti az elektromos áramot. Más szóval, minél nagyobb egy anyag vezetőképessége, annál jobb vezető.
Matematikailag:
σ = 1 / ρ
A vezetőképesség mértékegysége a Siemens per méter (S/m), amely az ohm per méter reciprok értéke. A Siemens (S) a konduktancia mértékegysége, ami az ellenállás reciproka.
A vezetőképesség fogalma különösen hasznos, amikor az anyagok áramvezető képességét hasonlítjuk össze. Magas vezetőképességű anyagokat használnak vezetékekhez és áramköri elemekhez, míg alacsony vezetőképességű anyagokat szigetelőként.
A fajlagos ellenállás az anyag árammal szembeni ellenállását fejezi ki, míg a vezetőképesség az áramvezető képességét mutatja meg. Reciprokai egymásnak.
Összefoglalva:
- Fajlagos ellenállás (ρ): Anyagra jellemző, mértékegysége Ωm. Minél nagyobb, annál rosszabb vezető.
- Ellenállás (R): Egy adott tárgyra jellemző, mértékegysége Ω. Függ az anyagtól, a hossztól és a keresztmetszettől.
- Vezetőképesség (σ): Anyagra jellemző, mértékegysége S/m. Minél nagyobb, annál jobb vezető. A fajlagos ellenállás reciproka.
Ezen fogalmak pontos megkülönböztetése kulcsfontosságú az anyagok elektromos tulajdonságainak mélyebb megértéséhez és a megfelelő anyagok kiválasztásához a különböző elektronikai és elektrotechnikai alkalmazásokhoz.
Szupervezetés: a nulla ellenállás világa

Amikor az elektromos ellenállásról beszélünk, nem hagyhatjuk figyelmen kívül azt az extrém esetet, amikor az ellenállás gyakorlatilag nullára csökken: ez a szupervezetés jelensége. A szupervezetés egy kvantummechanikai jelenség, amely bizonyos anyagokban rendkívül alacsony hőmérsékleten figyelhető meg.
Mi a szupervezetés?
A szupervezetés az a jelenség, amikor bizonyos anyagok (ún. szupravezetők) elektromos ellenállása hirtelen és teljesen nullára csökken egy kritikus hőmérséklet (Tc) alatt. Ezen a hőmérsékleten az anyag elveszíti minden ellenállását az elektromos árammal szemben, így az áram veszteség nélkül, időkorlát nélkül keringhet benne.
Ezenkívül a szupravezetők egy másik különleges tulajdonsággal is rendelkeznek: kiűzik magukból a mágneses mezőket (Meissner-effektus). Ez a jelenség felelős a mágneses lebegésért, ami látványos demonstrációja a szupervezetésnek.
A felfedezés és a típusok
A szupervezetést 1911-ben fedezte fel Heike Kamerlingh Onnes, amikor azt vizsgálta, hogyan változik a higany ellenállása rendkívül alacsony hőmérsékleten. Megfigyelte, hogy 4.2 Kelvin (-268.95 °C) hőmérsékleten a higany ellenállása hirtelen eltűnik.
Azóta számos más anyagot is felfedeztek, amelyek szupervezetővé válnak. Két fő típusát különböztetjük meg:
- I. típusú szupravezetők: Ezek általában tiszta fémek (pl. ólom, higany, ón), amelyek hirtelen, éles átmenettel válnak szupravezetővé egy kritikus hőmérséklet alatt. Jellemzően alacsony kritikus hőmérséklettel és mágneses mezővel rendelkeznek.
- II. típusú szupravezetők: Ezek általában ötvözetek vagy kerámia anyagok (pl. YBCO – ittrium-bárium-réz-oxid), amelyek magasabb kritikus hőmérséklettel és mágneses mezővel rendelkeznek. Ezek a típusok fokozatosabban válnak szupravezetővé, és képesek részlegesen beengedni a mágneses mezőket. A „magas hőmérsékletű szupravezetők” is ebbe a kategóriába tartoznak, bár a „magas” itt is még mindig rendkívül hideg hőmérsékletet jelent, jellemzően folyékony nitrogén hőmérsékletét (-196 °C) vagy az alattit.
Alkalmazások és jövőbeli lehetőségek
A szupervezetés rendkívüli tulajdonságai számos ígéretes alkalmazási lehetőséget kínálnak:
- Mágneses rezonancia képalkotás (MRI): A szupervezető mágnesek rendkívül erős és stabil mágneses mezőket hoznak létre, amelyek elengedhetetlenek az orvosi képalkotáshoz.
- Mágneses lebegésű vonatok (Maglev): A szupervezetés lehetővé teszi a vonatok lebegését a sín felett, kiküszöbölve a súrlódást és rendkívül nagy sebességet téve lehetővé.
- Erőátvitel: A nulla ellenállású vezetékek lehetővé tennék az elektromos energia veszteségmentes szállítását, jelentősen növelve az energiahatékonyságot.
- Elektronika: Szupervezető áramkörökkel rendkívül gyors és alacsony fogyasztású számítógépeket lehetne építeni.
- Fúziós reaktorok: A szupervezető mágnesek kulcsfontosságúak a plazma befogásához a kísérleti fúziós reaktorokban.
Bár a szupervezetés alkalmazása még mindig kihívásokkal teli a rendkívül alacsony hőmérséklet szükségessége miatt, a kutatások folyamatosan zajlanak a magasabb kritikus hőmérsékletű anyagok felfedezésére. Ha sikerülne szobahőmérsékleten működő szupravezetőt előállítani, az forradalmasítaná az energiaátvitelt, az elektronikát és számos más technológiai területet, alapjaiban változtatva meg az elektromos ellenállás szerepét a technológiában.
Gyakori tévhitek és félreértések az ellenállással kapcsolatban
Az elektromos ellenállás, bár alapvető fogalom, számos tévhit és félreértés forrása lehet, különösen a kezdők számára. Ezek tisztázása segíthet a mélyebb és pontosabb megértésben.
„Az ellenállás csak akadályozza az áramot”
Ez egy elterjedt, de hiányos megközelítés. Bár igaz, hogy az ellenállás korlátozza az áramot, sokkal több, mint puszta akadály. Az ellenállás valójában egy energiamenedzser. Ahogy az elektronok áthaladnak rajta, energiájuk egy részét hővé alakítják (Joule-hő). Ez az energiaátalakítás létfontosságú számos alkalmazásban, mint például a fűtés vagy az izzólámpák működése.
Ezenkívül az ellenállás kulcsfontosságú a feszültség és az áram szabályozásában, a jelek kondicionálásában és az áramkörök védelmében. Egy ellenállás nem csak „rossz”, hanem egy alapvető, aktív szerepet játszó alkatrész az elektronikus rendszerekben.
„Minden vezetéknek nulla az ellenállása”
Ez a kijelentés téves. Bár a vezetők, mint a réz vagy az alumínium, rendkívül alacsony fajlagos ellenállással rendelkeznek, soha nem nulla. Minden vezetéknek van valamennyi ellenállása, különösen ha hosszabbak vagy vékonyabbak. Ez az ellenállás okozza az energiaveszteséget hő formájában a távvezetékekben és az elektronikai áramkörökben.
Csak a szupravezetők rendelkeznek nulla ellenállással, de azok is csak rendkívül alacsony hőmérsékleten. A valóságban minden vezetéknek van egy bizonyos, bár gyakran elhanyagolható ellenállása, amelyet a precíziós alkalmazásokban figyelembe kell venni.
„Az ellenállás értéke állandó”
Bár a fix ellenállásokat úgy tervezik, hogy értékük stabil legyen, az ellenállás nem teljesen állandó. Ahogy korábban említettük, a hőmérséklet jelentősen befolyásolja az ellenállást. A legtöbb vezető ellenállása növekszik a hőmérséklet emelkedésével, míg a félvezetők és bizonyos speciális anyagok ellenállása csökkenhet.
Emellett az ellenállások értéke az öregedés, a mechanikai stressz vagy a túlzott terhelés (túlmelegedés) következtében is változhat. A gyártás során megadott tolerancia (pl. ±5%) is jelzi, hogy az ellenállás tényleges értéke eltérhet a névlegestől.
„A dióda vagy tranzisztor ellenállását az Ohm törvényével számolhatom”
Az Ohm törvénye (U = I ⋅ R) alapvetően az ohmos ellenállásokra vonatkozik, azaz azokra az alkatrészekre, amelyek ellenállása közel állandó a feszültség és az áram széles tartományában. A diódák és tranzisztorok azonban nemlineáris alkatrészek. Ellenállásuk drasztikusan változik a rájuk kapcsolt feszültségtől vagy az átfolyó áramtól függően. Például egy dióda ellenállása gyakorlatilag végtelen, amíg a nyitófeszültséget el nem éri, majd hirtelen nagyon alacsonyra csökken.
Bár lehet definiálni egy „dinamikus” vagy „differenciális” ellenállást ezekre az alkatrészekre egy adott munkaponton, a statikus Ohm törvénye közvetlenül nem alkalmazható a viselkedésük leírására.
„Az ellenállás csak egy passzív alkatrész”
Ez a kijelentés technikai értelemben igaz, mivel az ellenállások nem termelnek energiát, hanem disszipálják azt. Azonban az „passzív” szó gyakran azt a benyomást keltheti, hogy az ellenállások jelentéktelenek vagy kevéssé dinamikusak. A valóságban az ellenállások aktívan befolyásolják az áramkör működését: szabályozzák az áramot, osztják a feszültséget, generálnak hőt, részt vesznek időzítő és szűrő áramkörökben.
Az ellenállások „passzív” természete ellenére elengedhetetlenek az „aktív” alkatrészek, mint a tranzisztorok és integrált áramkörök megfelelő működéséhez. Az elektronikai rendszerekben betöltött szerepük messze túlmutat a puszta „passzív” jellegen.
Ezen tévhitek tisztázása segít abban, hogy az elektromos ellenállás fogalmát ne csak mechanikusan, hanem a fizikai valóság komplexitásában és az elektronikai alkalmazások sokszínűségében értsük meg.