A celluláris automata (CA) egy diszkrét modell, melyet komplex rendszerek viselkedésének szimulálására használnak. Lényegében egy cellákból álló rács, ahol minden cella egy véges számú állapot egyikében lehet. Az automata működésének kulcsa az, hogy minden cella állapota az időben diszkrét lépésekben változik, egy szabályrendszer alapján.
Ez a szabályrendszer figyelembe veszi a cella saját állapotát, valamint a szomszédos cellák állapotát is. A szomszédság definíciója változó lehet, de a leggyakoribb a közvetlen szomszédok figyelembe vétele. A szabályok determinisztikusak, ami azt jelenti, hogy egy adott cella és szomszédságának állapotára mindig ugyanaz az új állapot fog vonatkozni.
A celluláris automata ereje abban rejlik, hogy egyszerű szabályokból is rendkívül komplex és váratlan viselkedés jöhet létre.
A CA-k számos területen alkalmazhatók. Például, használják őket folyadékok áramlásának modellezésére, forgalmi dugók szimulálására, de akár biológiai rendszerek, például a sejtosztódás modellezésére is. A CA-k különösen hasznosak olyan rendszerekben, ahol a lokális kölcsönhatások globális viselkedést eredményeznek.
A modell definíciójának fontos része a rács dimenziója (1D, 2D, 3D, stb.), a cellák lehetséges állapotainak száma, a szomszédság definíciója és a szabályrendszer. A szabályrendszer gyakran egy táblázat formájában van megadva, amely minden lehetséges szomszédsági konfigurációhoz hozzárendeli a cella új állapotát.
A celluláris automata formális definíciója
A celluláris automata (CA) egy diszkrét modell, amelyet komplex rendszerek szimulálására használnak. Formális definíciója a következő elemekből áll össze:
- Cellák: A CA alapegységei, amelyek egy rácsot alkotnak. A rács lehet egy-, két-, vagy akár többdimenziós is. Minden cella egy adott időpillanatban egy meghatározott állapotban van.
- Állapotok: A cellák véges számú állapot valamelyikében lehetnek. A legegyszerűbb esetben ez csak két állapot (pl. „élő” vagy „halott”), de lehet több is.
- Szomszédság: Minden cellának van egy szomszédsága, amely a körülötte lévő cellák halmaza. A szomszédság definíciója határozza meg, hogy mely cellák befolyásolják egy adott cella állapotát. Például egy kétdimenziós rácsban a Moore-szomszédság a cellát körülvevő 8 cellát jelenti, míg a von Neumann-szomszédság a cella feletti, alatti, bal oldali és jobb oldali cellákat.
- Szabály: A CA működésének alapját képező szabály határozza meg, hogy egy cella állapota hogyan változik a szomszédságában lévő cellák állapotának függvényében. A szabály egy determinisztikus függvény, amely minden lehetséges szomszédsági állapotkombinációhoz egy új cellaállapotot rendel.
A CA működése diszkrét időbeli lépésekben történik. Minden lépésben minden cella állapota egyszerre frissül a szabály alapján. Ez azt jelenti, hogy a cellák állapota a szomszédságuk előző állapotától függ, és nem a jelenleg frissülő cellák állapotától.
A celluláris automata egy S = (L, Q, N, f) négyesként definiálható, ahol:
* L a cellák rácsa.
* Q az állapotok véges halmaza.
* N a szomszédsági sablon.
* f: Q|N| → Q az állapotátmeneti függvény (szabály).
A szabályt gyakran táblázatos formában adják meg, amely minden lehetséges szomszédsági konfigurációhoz megadja a cella új állapotát. Egyszerű szabályok is komplex viselkedést eredményezhetnek, ami a CA-k egyik legérdekesebb tulajdonsága. Például a Game of Life egy kétdimenziós CA, amelynek egyszerű szabályai ellenére meglepően komplex mintázatokat és viselkedést mutat.
A celluláris automaták széles körben alkalmazhatók különböző területeken, például:
- Fizika: folyadékdinamika, gázkinetika szimulációja
- Biológia: populációs modellek, sejtosztódás szimulációja
- Számítástechnika: párhuzamos számítások, képfeldolgozás
- Közgazdaságtan: piaci modellek, társadalmi viselkedés szimulációja
A CA-k ereje abban rejlik, hogy egyszerű szabályokból komplex viselkedést tudnak generálni, és alkalmasak olyan rendszerek modellezésére, amelyekben a lokális kölcsönhatások globális mintázatokat eredményeznek. A CA-k a nemlineáris dinamika és a komplexitáselmélet fontos eszközei.
A celluláris automata alapvető elemei: cellák, állapotok, szomszédság
A celluláris automata (CA) egy diszkrét modell, amelyet komplex rendszerek szimulálására használnak. Alapvető elemei a cellák, az állapotok és a szomszédság, melyek együttesen határozzák meg a modell működését.
A cellák a CA alapvető építőkövei. Képzeljük el őket egy rács pontjaiként, melyek lehetnek egy-, két- vagy akár többdimenziósak is. Minden cella egy adott állapotban lehet, amely egy véges halmazból kerül ki. Például, egy egyszerű esetben, a cella lehet „élő” vagy „halott”, amit 1-gyel illetve 0-val jelölhetünk. A cellák elrendezése a rácson meghatározza a CA topológiáját.
A cellák állapotának változása időben diszkrét lépésekben történik. Minden időpillanatban minden cella új állapotba kerül egy átmeneti szabály alapján. Ez a szabály figyelembe veszi az adott cella aktuális állapotát és a szomszédságában lévő cellák állapotait.
A szomszédság egy adott cella körül meghatározott cellák halmaza. A leggyakoribb szomszédsági típusok közé tartozik a Von Neumann szomszédság, amely egy cella négy közvetlen szomszédját (felül, alul, balra, jobbra) foglalja magába, és a Moore szomszédság, amely a nyolc szomszédos cellát (beleértve az átlósakat is) tartalmazza. A szomszédság mérete és alakja jelentősen befolyásolja a CA viselkedését.
Az átmeneti szabály egy függvény, amely meghatározza, hogy egy cella milyen állapotba kerül a következő időpillanatban, figyelembe véve a saját és a szomszédai állapotát. Ezt a szabályt általában egy táblázattal vagy egy egyenlettel adják meg. A szabály lehet determinisztikus, azaz minden bemeneti kombinációhoz egyértelműen meghatározott kimenet tartozik, vagy sztochasztikus, amikor a kimenet valószínűségi eloszlás alapján dől el.
A CA lényege abban rejlik, hogy egyszerű, lokális szabályok komplex, globális viselkedést eredményezhetnek.
Például, Conway Életjátéka egy híres kétdimenziós CA, ahol a cellák két állapotban lehetnek: „élő” vagy „halott”. Az átmeneti szabályok a következők:
- Egy élő cella túléli a következő generációt, ha 2 vagy 3 élő szomszédja van.
- Egy halott cella életre kel a következő generációban, ha pontosan 3 élő szomszédja van.
- Minden más esetben a cella a következő generációban halott lesz.
Ez a néhány egyszerű szabály rendkívül érdekes mintázatok kialakulásához vezethet, mint például stabil struktúrák, oszcillátorok és mozgó „űrhajók”.
A CA-k párhuzamosan működnek, ami azt jelenti, hogy minden cella állapotát egyidejűleg frissítik. Ez a párhuzamosság teszi őket alkalmassá komplex rendszerek szimulálására, ahol sok elem egyidejűleg lép kölcsönhatásba.
A CA-k széles körben alkalmazhatók különböző területeken, mint például a fizika, a biológia, a számítástechnika és a társadalomtudományok. Alkalmazzák őket folyadékdinamikai szimulációkra, ökológiai modellekre, képfeldolgozásra és a közlekedési forgalom modellezésére is.
A szomszédsági típusok: Von Neumann és Moore szomszédság
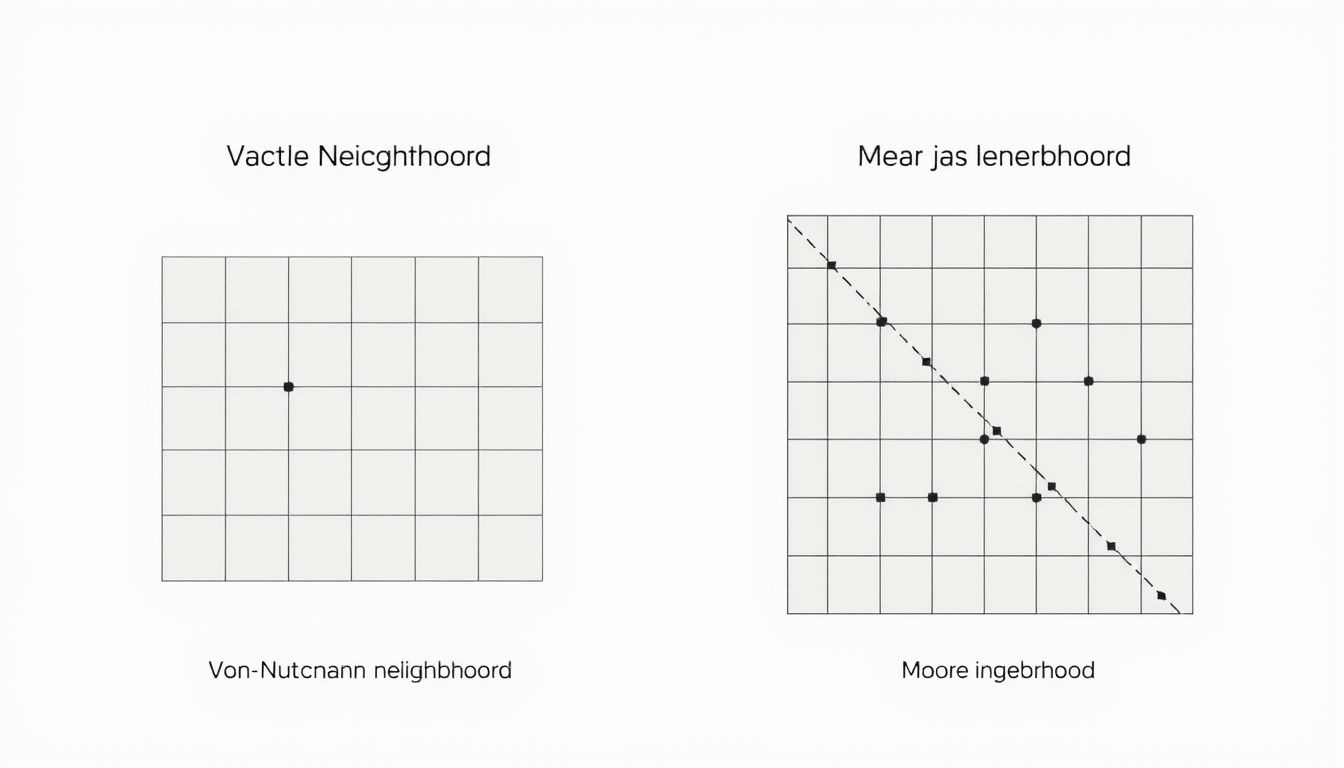
A celluláris automaták (CA) működésének egyik kulcsfontosságú eleme a szomszédság definíciója. Ez határozza meg, hogy egy adott cella állapotát mely más cellák állapota befolyásolja a következő időpillanatban. Két elterjedt szomszédsági típus létezik: a Von Neumann szomszédság és a Moore szomszédság.
A Von Neumann szomszédság egy adott cella négy közvetlen szomszédját foglalja magában: a felső, alsó, bal és jobb oldali cellákat. Tehát egy kétdimenziós rács esetén a (x,y) koordinátájú cella Von Neumann szomszédai a (x+1,y), (x-1,y), (x,y+1) és (x,y-1) koordinátájú cellák. Ez a szomszédsági típus a CA-ban gyakran olyan folyamatok modellezésére használatos, ahol a hatás közvetlenül, a fő irányok mentén terjed.
Ezzel szemben a Moore szomszédság a cella összes szomszédját figyelembe veszi, beleértve a diagonális szomszédokat is. Így egy (x,y) cella Moore szomszédsága az összes (x+i, y+j) cellát tartalmazza, ahol i és j értéke -1, 0 vagy 1, kivéve az (i=0, j=0) esetet, ami magát a cellát jelenti. Ez összesen 8 szomszédot jelent. A Moore szomszédság használata lehetővé teszi komplexebb minták és kölcsönhatások kialakulását a celluláris automatában, mivel a hatás nem csak a fő irányok mentén, hanem diagonálisan is terjed.
A választott szomszédsági típus jelentősen befolyásolja a CA viselkedését. Például, a Conway-féle Életjáték (Game of Life), egy híres celluláris automata, a Moore szomszédságot használja. Ezzel szemben, más CA-k, amelyek egyszerűbb folyamatokat modelleznek, hatékonyabban működhetnek a Von Neumann szomszédsággal.
A szomszédsági típus megválasztása kulcsfontosságú a CA által modellezett jelenség tulajdonságainak megfelelő visszaadásához.
A szomszédsági típus mellett a cellák állapota (például bináris, vagy többértékű), és az alkalmazott szabályok is meghatározzák a CA viselkedését. A szabályok határozzák meg, hogy egy cella állapota hogyan változik a szomszédai állapotának függvényében a következő időpillanatban. Ezek a szabályok lehetnek egyszerűek vagy komplexek, és ezek adják a CA dinamikájának alapját.
Végső soron, a Von Neumann és Moore szomszédság csak két példa a lehetséges szomszédsági típusok közül. Léteznek más, exotikusabb szomszédsági definíciók is, amelyek speciális alkalmazásokhoz lettek kifejlesztve. A megfelelő szomszédsági típus kiválasztása a modellezett probléma természetétől függ.
A szabályok szerepe a celluláris automata működésében
A celluláris automata (CA) működésének szíve a szabályrendszer, amely meghatározza a sejtek állapotának változását az idő múlásával. Ezek a szabályok lokálisak, ami azt jelenti, hogy egy adott sejt új állapota kizárólag a közvetlen környezetének (a szomszédos sejtek állapotának) függvénye, és a sejt saját korábbi állapotától függ.
A szabályok általában táblázatos formában vannak megadva. Minden lehetséges szomszédsági konfigurációhoz (például a bal oldali, a jobb oldali és a középső sejt állapota) tartozik egy szabály, amely megadja, hogy a középső sejt milyen új állapotot vesz fel a következő időpillanatban. A CA működése során minden egyes sejt egyszerre, szinkron módon frissíti az állapotát a saját környezetére vonatkozó szabály alapján.
A szabályrendszer meghatározó abban, hogy a CA milyen viselkedést mutat. Egyes szabályok stabilitást eredményeznek, ahol a rendszer gyorsan egy állandó, nem változó állapotba kerül. Más szabályok periodikus viselkedést eredményeznek, ahol a rendszer egy ismétlődő mintázatot mutat. A legérdekesebbek talán azok a szabályok, amelyek komplex, kaotikus viselkedést generálnak, és váratlan, bonyolult mintázatok alakulnak ki.
A szabályok egyszerűsége ellenére a celluláris automaták képesek rendkívül komplex viselkedést produkálni, ami rávilágít arra, hogy a lokális interakciók globális szinten milyen meglepő eredményekhez vezethetnek.
A szabályok megválasztása kulcsfontosságú a CA által modellezett jelenség szempontjából. Például, ha egy CA-t tűzterjedés modellezésére használunk, akkor a szabályoknak tükrözniük kell a tűz terjedésének fizikai törvényeit: a tűz átterjed a szomszédos éghető területekre, a szél befolyásolja a terjedés irányát, stb. A helyes szabályok kiválasztása iteratív folyamat lehet, amely során a szabályokat finomítjuk, amíg a CA viselkedése hűen tükrözi a modellezett valóságot.
A szabályok típusai is befolyásolják a CA viselkedését. Például, a totális szomszédsági szabályok esetében a sejt új állapota a szomszédos sejtek állapotának összegétől függ, nem pedig az egyes szomszédok konkrét állapotától. Ez a fajta szabályrendszer gyakran vezet szimmetrikus, organikus mintázatok kialakulásához.
A CA-k sokfélesége nagyrészt a szabályrendszer változatosságából ered. A szabályok apró módosításai is drámai változásokat eredményezhetnek a CA viselkedésében, ami lehetővé teszi a különböző jelenségek modellezését a természetben és a társadalomban.
Globális átmeneti függvény és annak hatása
A celluláris automata (CA) működésének kulcsa a globális átmeneti függvény. Ez a függvény határozza meg, hogy a CA egy adott állapotból hogyan jut el a következő állapotba. A globális átmeneti függvény valójában a lokális átmeneti szabályok együttes alkalmazásának eredménye az automata minden egyes cellájára.
Minden cella új állapota a saját és a szomszédos cellák aktuális állapotától függ, ezt a kapcsolatot a lokális átmeneti szabály definiálja. A globális átmeneti függvény tehát nem egyetlen, központi számítás, hanem a lokális szabályok párhuzamos, elosztott alkalmazása. Ez a párhuzamosság teszi lehetővé, hogy a CA-k komplex, emergenciális viselkedést mutassanak, még egyszerű lokális szabályok mellett is.
A globális átmeneti függvény hatása drasztikusan eltérhet a lokális szabályok egyszerű összegzésétől. A lokális interakciók globális mintázatokat hozhatnak létre, amiket nehéz lenne megjósolni a lokális szabályok ismeretében. Például a „Game of Life” nevű CA-ban, ahol a lokális szabályok nagyon egyszerűek (egy cella akkor marad életben, ha két vagy három szomszédja él, egyébként meghal, és egy üres cella akkor éled újjá, ha pontosan három szomszédja él), meglepően komplex struktúrák és mozgások alakulhatnak ki.
A globális átmeneti függvény tehát nem csupán a lokális szabályok összessége, hanem egy emergenciális folyamat, amely új, váratlan viselkedéseket hoz létre.
A globális átmeneti függvény determinisztikus volta ellenére (azaz ugyanazok a kezdeti feltételek mindig ugyanazt a végeredményt adják), a CA-k viselkedése gyakran kaotikus. Ez azt jelenti, hogy a kezdeti feltételek apró változásai is drámai különbségeket eredményezhetnek a későbbi állapotokban. Ezt a jelenséget a pillangóhatáshoz lehet hasonlítani.
A globális átmeneti függvény tanulmányozása kritikus fontosságú a CA-k viselkedésének megértéséhez és a különböző jelenségek modellezéséhez, a forgalomirányítástól a társadalmi viselkedésig.
A szabályok leírásának módszerei: táblázatok, képletek, algoritmusok
A celluláris automaták (CA) működését meghatározó szabályok leírására többféle módszer létezik. Ezek a módszerek a szabályok komplexitásától és a kívánt részletességtől függően változnak.
A legközvetlenebb módszer a táblázat. Egy ilyen táblázat minden lehetséges szomszédsági konfigurációt felsorol, és megadja, hogy az adott konfiguráció esetén az adott cella milyen állapotba kerül a következő időpillanatban. Például, egy elemi CA (1D, 2-állapotú, 3-cellás szomszédság) esetén 2^3 = 8 lehetséges konfiguráció van, így a táblázat 8 sort tartalmazna. A táblázat egyszerűen értelmezhető, de nagyméretű szomszédságok vagy sok állapot esetén gyorsan kezelhetetlenné válik.
A képletek egy tömörebb módszert kínálnak a szabályok leírására. A képletek matematikai vagy logikai kifejezések formájában adják meg, hogy egy cella új állapota hogyan függ a szomszédai állapotától. Például, egy egyszerű képlet meghatározhatja, hogy egy cella akkor kerül 1-es állapotba, ha legalább két szomszédja 1-es állapotban van. A képletek általában tömörebbek, mint a táblázatok, és lehetővé teszik a szabályok általánosabb leírását.
A CA szabályok leírására használt algoritmusok lehetővé teszik a legösszetettebb és legrugalmasabb megközelítést.
Az algoritmusok egy programozási nyelven megírt kód formájában írják le a szabályokat. Ez a módszer különösen hasznos, ha a szabályok bonyolult logikát tartalmaznak, például feltételeket, ciklusokat vagy rekurziót. Az algoritmusok lehetővé teszik a szabályok dinamikus változtatását is, például a CA futása közben. Például, egy algoritmus meghatározhatja, hogy egy cella új állapota hogyan függ a szomszédai állapotától, de figyelembe veheti a cella korábbi állapotát is.
A választott módszertől függetlenül, a szabályok egyértelmű és pontos leírása elengedhetetlen a CA viselkedésének megértéséhez és reprodukálásához.
Egydimenziós celluláris automaták: Elementary Cellular Automata (ECA)

Az egydimenziós celluláris automaták (CA) a celluláris automaták legegyszerűbb típusai. Ezekben a CA-kban a sejtek egyetlen sorban helyezkednek el, és állapotuk csak a közvetlen szomszédaiktól függ.
A legegyszerűbb egydimenziós CA-kat Elementary Cellular Automata (ECA)-nak nevezzük. Az ECA-kban minden sejt két lehetséges állapotot vehet fel: 0 (inaktív) vagy 1 (aktív). Egy adott sejt új állapota a közvetlen szomszédainak (bal oldali szomszéd, maga a sejt és a jobb oldali szomszéd) állapotától függ. Mivel 3 sejtnek 23 = 8 lehetséges kombinációja van, és minden kombinációhoz tartozik egy új sejtállapot (0 vagy 1), ezért összesen 28 = 256 különböző ECA létezik.
Minden ECA-hoz egy szabályt rendelünk, amely meghatározza, hogy egy sejt hogyan változtatja meg az állapotát a szomszédai alapján. A szabályokat általában egy számmal jelöljük, melyet binárisan ábrázolva kapjuk meg a 8 kimeneti állapotot. Például, a 30-as szabály (binárisan 00011110) azt jelenti, hogy a sejt akkor lesz aktív (1), ha a szomszédai (a bal oldali, a sejt maga és a jobb oldali) a következő konfigurációkban vannak: 011, 100, 101 vagy 110. Minden más esetben a sejt inaktív (0) marad.
Az ECA-k egyszerűsége ellenére meglepően komplex viselkedést mutathatnak.
Az ECA-k működését általában úgy szemléltetjük, hogy egy sor kezdeti konfigurációból (initial state) indulunk ki, majd iteratívan alkalmazzuk a szabályt minden sejt minden generációjára. Az eredmény egy minta, ami megmutatja, hogyan változik a sejtek állapota az idő múlásával. Ezek a minták lehetnek egyszerűek (pl. homogén állapot vagy periodikus ismétlődés), de lehetnek rendkívül komplexek és kaotikusak is. Egyes ECA-k, mint például a 30-as szabály, látszólag véletlenszerű mintákat produkálnak, és alkalmazhatók véletlenszám-generátorokban.
Az ECA-k tanulmányozása fontos a komplex rendszerek megértéséhez. Bár egyszerű modellek, képesek komplex viselkedést produkálni, ami segít megérteni a bonyolultabb rendszerekben lejátszódó folyamatokat. A Wolfram-féle osztályozás szerint az ECA-k négy osztályba sorolhatók a viselkedésük alapján: homogén, periodikus, kaotikus és komplex.
Wolfram kódok és az ECA szabályok osztályozása
A celluláris automaták (CA) tanulmányozásában kulcsszerepet játszik a szabályok osztályozása, ami különösen fontos az elemi celluláris automaták (ECA) esetében. Stephen Wolfram úttörő munkája során egy egyszerű, de hatékony módszert dolgozott ki az ECA szabályok azonosítására: a Wolfram-kódot.
Az ECA-k 1 dimenziós CA-k, ahol minden cella két állapotot vehet fel (általában 0 és 1), és a következő állapotot a közvetlen szomszédai (bal és jobb) és saját maga aktuális állapota határozza meg. Ez azt jelenti, hogy 23 = 8 lehetséges szomszédsági konfiguráció létezik. A szabály lényegében egy táblázat, amely megadja, hogy az egyes konfigurációkhoz melyik új állapot tartozik.
A Wolfram-kód úgy jön létre, hogy az összes lehetséges szomszédsági konfigurációt (111, 110, 101, 100, 011, 010, 001, 000) sorba rendezzük, és az ezekhez a konfigurációkhoz tartozó új állapotokat (0 vagy 1) ebben a sorrendben egymás után írjuk. Az így kapott bináris számot ezután decimális számmá alakítjuk, ami a Wolfram-kódot adja meg. Mivel 8 bitünk van, a Wolfram-kód értéke 0 és 255 között lehet.
Például, ha egy szabály a következő:
- 111 -> 0
- 110 -> 1
- 101 -> 1
- 100 -> 0
- 011 -> 1
- 010 -> 0
- 001 -> 1
- 000 -> 0
Akkor a bináris reprezentáció 01101010, ami decimálisan 106. Tehát ennek a szabálynak a Wolfram-kódja 106.
A Wolfram-kód lehetővé teszi az ECA szabályok egyszerű és egyértelmű azonosítását. Azonban, mivel a szomszédsági konfigurációk sorrendje rögzített, bizonyos szabályok szimmetrikusak vagy egyszerűen egymás tükörképei lehetnek. Ezért Wolfram az ECA szabályokat négy osztályba sorolta, viselkedésük alapján:
- 1. osztály: Homogén állapotba konvergálnak (minden cella azonos értéket vesz fel).
- 2. osztály: Egyszerű, periodikus struktúrákat eredményeznek.
- 3. osztály: Káoszos, pszeudo-véletlenszerű mintázatokat hoznak létre.
- 4. osztály: Komplex, lokalizált struktúrákat (pl. „gliderek”) generálnak, amelyek interakcióba léphetnek egymással. Ezek a szabályok gyakran mutatnak a legérdekesebb viselkedést, és potenciálisan képesek univerzális számításra.
A Wolfram-kód egy praktikus eszköz az ECA szabályok azonosítására, de a viselkedésük osztályozása mélyebb betekintést nyújt a celluláris automaták komplexitásába és potenciális alkalmazásaiba.
A 4. osztályú szabályok különösen érdekesek, mert határterületet képeznek a rendezettség és a káosz között. Bár a Wolfram-féle osztályozás hasznos kiindulópont, nem mindig egyértelmű, hogy egy adott szabály melyik osztályba tartozik, és a besorolás néha szubjektív lehet.
A Wolfram-kód és az ECA szabályok osztályozása alapvető fontosságú a celluláris automaták elméletének és gyakorlati alkalmazásainak megértéséhez. Ezek az eszközök lehetővé teszik a kutatók számára, hogy rendszerezzék, összehasonlítsák és elemezzék a különböző szabályok viselkedését, ami hozzájárulhat új algoritmusok és számítási modellek fejlesztéséhez.
Kétdimenziós celluláris automaták: Conway’s Game of Life
A celluláris automaták (CA) egy különösen érdekes és széles körben alkalmazott modellcsalád a komplex rendszerek szimulációjára. A CA alapvetően egy diszkrét térben és időben működő, egyszerű szabályok alapján fejlődő rendszer.
A kétdimenziós celluláris automaták talán legismertebb példája Conway’s Game of Life, azaz az Életjáték. Ez a modell egy végtelen, kétdimenziós rácsot használ, ahol minden cella két állapotban lehet: élő (1) vagy halott (0). A játék nem igényel játékos általi beavatkozást; a kezdeti konfigurációtól függően az állapotok az idő múlásával a szabályok szerint változnak.
A Game of Life működését négy egyszerű szabály határozza meg, amelyek minden egyes cellára egyidejűleg alkalmazásra kerülnek minden időlépésben. A szabályok a cella nyolc szomszédjának (a közvetlen szomszédok és az átlósan elhelyezkedő cellák) állapotát veszik figyelembe:
- Egy élő cella túléli a következő generációt, ha pontosan két vagy három élő szomszédja van.
- Egy élő cella elpusztul alulnépesedés miatt, ha kevesebb, mint két élő szomszédja van.
- Egy élő cella elpusztul túlnépesedés miatt, ha több, mint három élő szomszédja van.
- Egy halott cella életre kel a következő generációban, ha pontosan három élő szomszédja van.
Ezek a látszólag egyszerű szabályok meglepően komplex és érdekes mintázatokat eredményezhetnek. A Game of Life képes önismétlődő struktúrák, oszcilláló konfigurációk (például a „villogó” vagy „periodikus” mintázatok) és mozgó struktúrák (például a „sikló”) létrehozására.
Az Életjáték Turing-teljes, ami azt jelenti, hogy elvileg bármilyen számítást képes elvégezni, amelyet egy számítógép is.
A Game of Life nem csak egy szórakoztató játék, hanem fontos betekintést nyújt az önszerveződésbe, a komplex viselkedésbe és az emergenciába. Megmutatja, hogy egyszerű szabályok hogyan vezethetnek bonyolult és váratlan mintázatokhoz.
A modell népszerűségéhez hozzájárul az is, hogy könnyen implementálható számítógépen, és vizuálisan is rendkívül látványos. Számos online szimulátor és program létezik, amelyek lehetővé teszik a felhasználók számára, hogy kísérletezzenek különböző kezdeti konfigurációkkal és megfigyeljék a rendszer fejlődését.
Bár a Game of Life egy determinisztikus rendszer (azaz a jövőbeli állapot teljes mértékben meghatározott a jelenlegi állapottól), a létrejövő mintázatok előrejelzése gyakran rendkívül nehéz. Ez a tulajdonság is hozzájárul a modell vonzerejéhez és a komplex rendszerek kutatásában betöltött jelentőségéhez.
A Game of Life szabályai és a belőlük fakadó komplex viselkedés
A Game of Life, John Conway által 1970-ben megalkotott celluláris automata, talán a legismertebb példa erre a modellre. Lényegében egy nulla játékosú játék, ahol a rendszer fejlődését kezdeti állapota és néhány egyszerű szabály határozza meg.
A játék egy kétdimenziós rácsban játszódik, ahol minden cella vagy élő (1) vagy halott (0) állapotban lehet. A rács elméletileg végtelen, de a gyakorlatban véges méretű területeken vizsgáljuk.
A játék minden egyes lépésében (generációjában) minden cella állapota a következő szabályok szerint változik:
- Egy élő cella, amelynek kevesebb, mint két élő szomszédja van, meghal (alulnépesedés).
- Egy élő cella, amelynek két vagy három élő szomszédja van, életben marad a következő generációban.
- Egy élő cella, amelynek több, mint három élő szomszédja van, meghal (túlnépesedés).
- Egy halott cella, amelynek pontosan három élő szomszédja van, életre kel (reprodukció).
A szomszédság általában a Moore-szomszédság, ami azt jelenti, hogy egy cellának nyolc szomszédja van: a közvetlen vízszintes, függőleges és átlós szomszédok.
A Game of Life egyszerű szabályai ellenére meglepően komplex és változatos mintázatokat hozhat létre.
Egyes mintázatok stabilak, azaz nem változnak a következő generációban. Ilyen például a „blokk”, egy 2×2-es élő cellákból álló négyzet.
Más mintázatok oszcillálnak, azaz periodikusan ismétlődnek. A leggyakoribb példa a „villogó”, egy két cellából álló sor, ami vízszintes és függőleges helyzet között váltakozik.
Vannak mozgó mintázatok is, mint például a „vitorlázó”, ami generációról generációra átlósan mozog a rácson. Ezek a mintázatok különösen érdekesek, mert a Game of Life-ban Turing-teljességet mutatnak, ami azt jelenti, hogy elméletileg bármilyen számítást el lehet végezni velük.
A Game of Life nem csak egy játék, hanem egy modell, ami a komplex rendszerek viselkedésének megértéséhez is hozzájárul. Megmutatja, hogy egyszerű szabályokból is bonyolult és váratlan jelenségek születhetnek.
A celluláris automaták párhuzamos működése
A celluláris automaták (CA) párhuzamos működése az, ami igazán megkülönbözteti őket a hagyományos számítási modellektől. Minden egyes cella egyszerre, a többi cellától függetlenül frissíti az állapotát.
Ez a párhuzamosság a CA egyik legfontosabb jellemzője. A frissítési szabály alkalmazása minden cellára egyszerre történik, ami hatalmas számítási teljesítményt eredményezhet, különösen nagyméretű CA-k esetén.
A párhuzamos működés azt jelenti, hogy az n+1-edik időpillanatbeli állapot minden cellára az n-edik időpillanatbeli állapot alapján számítódik ki. Nincs függőség az egyes cellák frissítései között ugyanazon időpillanaton belül. Ez lehetővé teszi a CA-k hatékony szimulációját párhuzamos számítástechnikai architektúrákon, például GPU-kon.
A globális viselkedés, komplex mintázatok a lokális szabályok és a párhuzamos frissítés kölcsönhatásából erednek.
Azonban a párhuzamos frissítés kihívásokat is jelenthet. Például, a frissítési sorrend befolyásolhatja a CA viselkedését, ha nem szigorúan szimultán a frissítés. Ezért a legtöbb CA modell szinkron frissítést feltételez, ahol minden cella egyszerre, egy központi órajelre frissül.
A CA-k párhuzamos jellege lehetővé teszi, hogy nagyon összetett rendszereket modellezzenek viszonylag egyszerű szabályokkal. Ez teszi őket népszerűvé különböző területeken, mint például a fizikában, biológiában és számítástechnikában.
A celluláris automaták alkalmazási területei: fizika, biológia, számítástechnika
A celluláris automaták (CA) egyszerű szabályokon alapuló modellek, amelyek meglepően komplex viselkedést képesek produkálni. Ez a tulajdonságuk teszi őket rendkívül vonzóvá a különböző tudományterületeken, különösen a fizikában, a biológiában és a számítástechnikában.
A fizikában a CA-k a komplex rendszerek, például a folyadékok, gázok és szilárd anyagok modellezésére használhatók. Például, a gázok viselkedését szimulálhatjuk úgy, hogy a CA cellái gázrészecskéket reprezentálnak, és a szabályok a részecskék közötti ütközéseket és mozgásokat írják le. Ezek a szimulációk segíthetnek megérteni a turbulencia, a fázisátalakulások és más komplex fizikai jelenségek hátterét.
A biológiában a CA-k a sejtek közötti kölcsönhatások, a populációk dinamikája és a morfogenezis (a szervek és szövetek kialakulása) modellezésére alkalmazhatók. A sejt alapú modellezés során minden sejt egy CA cellát képvisel, és a szabályok a sejtosztódást, a differenciálódást és a sejtek közötti kommunikációt írják le. Ezek a modellek segíthetnek megérteni a rákos daganatok növekedését, a vírusok terjedését és az ökoszisztémák működését.
A celluláris automaták alkalmasak komplex rendszerek modellezésére a fizikában, biológiában és számítástechnikában, mivel egyszerű szabályok alapján is képesek bonyolult viselkedést produkálni.
A számítástechnikában a CA-k a párhuzamos számítások, a kriptográfia és a mesterséges intelligencia területén találnak alkalmazásra. A párhuzamos számítások során a CA cellái processzorokat képviselhetnek, és a szabályok a processzorok közötti kommunikációt és adatok áramlását írják le. A CA-k használhatók véletlenszám-generálásra is, ami a kriptográfiában elengedhetetlen. Emellett a CA-k felhasználhatók mesterséges neurális hálózatok modellezésére is, ahol a cellák neuronokat, a szabályok pedig a neuronok közötti kapcsolatokat és a jelátvitelt reprezentálják.
Egy konkrét példa a biológiában a „Game of Life” nevű CA, amit John Conway alkotott meg. Bár nagyon egyszerű szabályokon alapul, képes komplex mintázatokat létrehozni, amelyek szimulálják a sejtek növekedését és pusztulását. A „Game of Life” demonstrálja, hogy egyszerű szabályok is képesek komplex, emergensen megjelenő viselkedést eredményezni.
Egy másik példa a fizikában a rácsgáz-automata, amelyet folyadékok áramlásának szimulálására használnak. Ebben az automatában a cellák részecskék pozícióit képviselik, és a szabályok a részecskék mozgását és ütközéseit írják le. A rácsgáz-automaták hatékony eszközt jelentenek a folyadékok viselkedésének tanulmányozására, különösen olyan esetekben, amikor a hagyományos numerikus módszerek nehézségekbe ütköznek.
A celluláris automaták korlátai és kihívásai
A celluláris automaták, bár rendkívül sokoldalú modellek, számos korláttal és kihívással szembesülnek. Az egyik legnagyobb nehézség a megfelelő szabályok megtalálása egy adott jelenség modellezéséhez. A szabályok tervezése gyakran időigényes kísérletezést igényel, és nincs garancia arra, hogy a talált szabályok valóban tükrözik a vizsgált rendszer komplexitását.
A CA-k egy másik korlátja a számítási igény. A nagyobb, komplexebb automaták szimulációja komoly számítási erőforrásokat igényelhet, különösen hosszú időtartamokra vetítve. Ez korlátozza az alkalmazhatóságukat a valós idejű szimulációkban vagy a nagyméretű rendszerek modellezésében.
A determinisztikus szabályok ellenére a CA-k viselkedése gyakran előrejelezhetetlen, ami megnehezíti a modell eredményeinek értelmezését és validálását.
Ezenkívül a CA-k diszkrét jellegük miatt nem feltétlenül alkalmasak a folytonos jelenségek pontos modellezésére. Bár a finomabb cellaméret segíthet, ez tovább növeli a számítási igényt.
Végül, a celluláris automaták érzékenyek lehetnek a kezdeti feltételekre. Egy apró változás a kezdeti konfigurációban drasztikusan eltérő viselkedéshez vezethet, ami megnehezíti a modell robusztusságának biztosítását.