A binárisan kódolt decimális (BCD) egy számábrázolási rendszer, amely a decimális számjegyeket bináris formában tárolja. Eltér a hagyományos bináris ábrázolástól, ahol a teljes számot alakítjuk át binárissá. A BCD esetében minden egyes decimális számjegy külön-külön kerül bináris formába kódolásra.
Gyakran használják olyan alkalmazásokban, ahol a decimális értékek pontos ábrázolása kritikus, és a bináris-decimális átalakítás pontossága fontosabb a számítási hatékonyságnál. Ilyen lehet például a pénzügyi számítások vagy a digitális kijelzők vezérlése.
A leggyakoribb BCD kódolás a 8421 BCD, ahol minden decimális számjegyet egy 4 bites bináris számmal ábrázolunk. Ebben a kódolásban a bitek súlyozása 8, 4, 2 és 1. Például a 3-as decimális számjegy a 0011 bináris kóddal, a 7-es pedig a 0111 bináris kóddal van ábrázolva.
Érdemes megjegyezni, hogy a 8421 BCD csak a 0-tól 9-ig terjedő decimális számjegyeket használja ki a 4 bites bináris kódolás teljes potenciáljából. A 1010-től 1111-ig terjedő kódokat nem használjuk, mivel ezek nem felelnek meg decimális számjegyeknek.
A BCD előnye, hogy a decimális számok megjelenítése és kezelése egyszerűbbé válik, mivel közvetlenül a decimális számjegyekkel dolgozunk a bináris reprezentációban.
Vannak más BCD kódolások is, például a 3-as többletkód, ahol minden decimális számjegyhez hozzáadunk 3-at, mielőtt binárissá alakítanánk. Ez a kódolás hasznos lehet bizonyos aritmetikai műveletek egyszerűsítésére.
A BCD használatának egyik hátránya, hogy több memóriát igényelhet, mint a hagyományos bináris ábrázolás, különösen nagyobb számok esetén. Ennek oka, hogy minden decimális számjegyhez külön 4 bitet kell tárolni, míg a bináris ábrázolás hatékonyabban használja ki a rendelkezésre álló biteket.
A BCD definíciója és célja
A binárisan kódolt decimális (BCD) egy számábrázolási rendszer, amelyben minden decimális számjegyet külön-külön bináris számokkal reprezentálunk. Ahelyett, hogy egy teljes számot alakítanánk át bináris formátumba, a BCD minden egyes számjegyet egy különálló bináris kóddal helyettesít. Leggyakrabban a 8421-es BCD kódot használják, ahol minden decimális számjegyet egy négybites bináris számmal ábrázolunk, melynek értéke 0-tól 9-ig terjed.
Például, a 127 decimális szám BCD formátumban a következőképpen néz ki: 0001 0010 0111. Láthatjuk, hogy minden decimális számjegy (1, 2, és 7) a saját négybites bináris megfelelőjével van ábrázolva. Ezzel szemben, a hagyományos bináris ábrázolásban a 127 decimális szám 01111111 lenne.
A BCD elsődleges célja, hogy megkönnyítse a decimális számokkal végzett műveleteket a digitális rendszerekben, különösen azokban az alkalmazásokban, ahol az emberek által olvasható formátum és a számítógépes feldolgozás közötti konverzió gyakori és kritikus fontosságú. Ez különösen hasznos pénzügyi alkalmazásokban, ahol a pontos decimális ábrázolás elengedhetetlen.
A BCD használata kiküszöböli a bináris-decimális átalakításból adódó kerekítési hibákat, mivel minden decimális számjegyet pontosan reprezentál.
A BCD használatának előnyei közé tartozik a könnyű konverzió a decimális és bináris formátumok között, valamint a jobb olvashatóság a bináris ábrázoláshoz képest. Ugyanakkor hátránya, hogy kevésbé hatékonyan használja a memóriát, mivel négy bitet használ minden decimális számjegyhez, még akkor is, ha a négy biten ábrázolható értékek egy része (10-15) nincs kihasználva.
A BCD alkalmazásai széleskörűek: megtalálható digitális órákban (ahol a számjegyek közvetlenül BCD formátumban jelennek meg), számológépekben, mérőműszerekben és olyan rendszerekben, ahol a decimális pontosság elsődleges szempont. Például, egy digitális órában a BCD lehetővé teszi, hogy a kijelzőn látható számjegyek közvetlenül tükrözzék a tárolt időértéket, anélkül, hogy bonyolult bináris-decimális átalakításra lenne szükség.
Bár a modern számítógépek többsége a bináris ábrázolást használja a számításokhoz, a BCD továbbra is fontos szerepet játszik bizonyos speciális területeken, ahol a decimális pontosság és a könnyű konverzió kulcsfontosságú.
A BCD történeti háttere és fejlődése
A binárisan kódolt decimális (BCD) ábrázolás története szorosan összefonódik a korai számítógépek és elektronikus számológépek megjelenésével. A BCD-t azért fejlesztették ki, hogy egyszerűsítsék a decimális számok bináris rendszerekben való tárolását és feldolgozását. Ez különösen fontos volt a korai időszakban, amikor a számítógépek még nem voltak elég hatékonyak a bonyolult bináris aritmetikai műveletek elvégzésére.
A BCD korai formái már a 19. században megjelentek, mechanikus számológépekben. Ezek a gépek gyakran közvetlenül decimális számjegyekkel dolgoztak, és a BCD kódolás lehetővé tette, hogy az egyes számjegyeket könnyebben ábrázolják és manipulálják.
A BCD elterjedése az elektronikus számítógépek megjelenésével felgyorsult. Az ENIAC, az egyik első elektronikus számítógép, BCD-t használt a számok tárolására. Ez leegyszerűsítette a bemeneti adatok decimális formátumban történő bevitelét és a kimeneti eredmények decimális formátumban történő megjelenítését.
A hatvanas és hetvenes években a BCD széles körben elterjedt az üzleti alkalmazásokban és a nagyszámítógépekben, ahol a pontos decimális számítások elengedhetetlenek voltak. A banki rendszerek, a pénzügyi szoftverek és a leltárkezelő rendszerek gyakran használták a BCD-t a pénzügyi adatok kezelésére.
A BCD egyik legfontosabb előnye a decimális számítások pontossága és a kerekítési hibák minimalizálása.
A mikroprocesszorok megjelenésével a BCD továbbra is fontos maradt, különösen azokban az alkalmazásokban, ahol a decimális aritmetika elengedhetetlen volt. Számos mikroprocesszor, például az Intel 8080, rendelkezett beépített BCD aritmetikai utasításokkal.
Bár a bináris aritmetika hatékonyságának növekedésével a BCD használata az általános célú számítógépekben csökkent, továbbra is fontos szerepet játszik speciális alkalmazásokban, például a pénzügyi rendszerekben, a mérőműszerekben és a beágyazott rendszerekben, ahol a pontos decimális számítások kritikusak.
A BCD különböző típusai: Csomagolt és csomagolatlan BCD
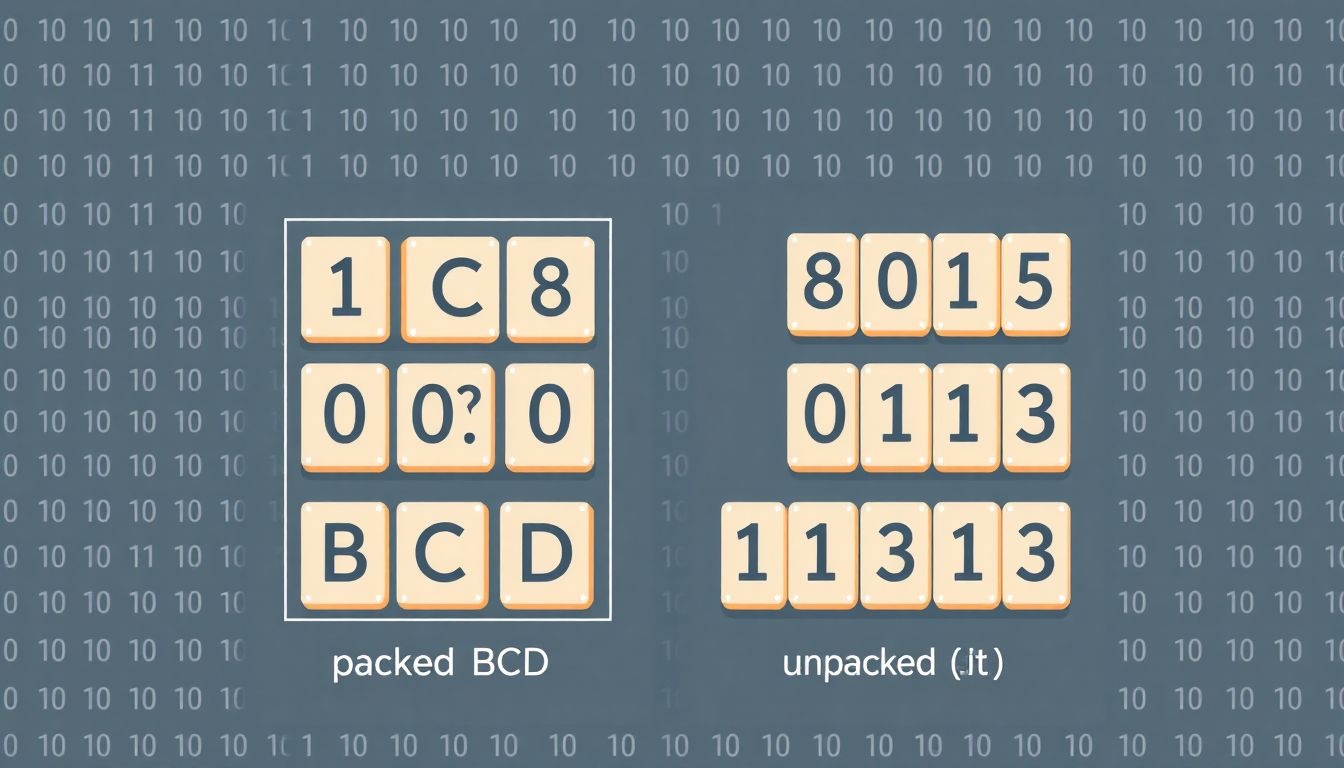
A binárisan kódolt decimális (BCD) számábrázolás különböző implementációkban létezik, amelyek közül a leggyakoribbak a csomagolt BCD és a csomagolatlan BCD. Mindkét típus a decimális számjegyeket bináris formában tárolja, de a tárolás módja eltérő, ami befolyásolja a memóriahasználatot és a feldolgozási sebességet.
A csomagolatlan BCD esetében minden egyes decimális számjegy egy teljes bájtot foglal el. Mivel egy decimális számjegy 0 és 9 közötti értéket vehet fel, 4 bit elegendő a reprezentációjához. A maradék 4 bitet általában nullával töltik fel, vagy más, nem releváns információt tárolnak benne. Például, a 9-es számjegyet a csomagolatlan BCD-ben a 0000 1001 bájttal ábrázoljuk. Ez a módszer egyszerű, de pazarló a memóriát tekintve, mivel a bájtok felét nem használja ki hatékonyan. A csomagolatlan BCD-t gyakran használják olyan rendszerekben, ahol a memória nem korlátozott erőforrás, és a feldolgozási sebesség kritikus.
Ezzel szemben a csomagolt BCD hatékonyabban használja a memóriát. Ebben a formátumban két decimális számjegyet tárolunk egyetlen bájtban. Mivel egy bájt 8 bitet tartalmaz, és egy decimális számjegyhez 4 bit szükséges, egy bájt pontosan két számjegy tárolására alkalmas. Például, a 29-es számot a csomagolt BCD-ben a 0010 1001 bájttal ábrázoljuk. Ez a módszer jelentősen csökkenti a memóriahasználatot, különösen nagy számok esetén. A csomagolt BCD-t gyakran alkalmazzák olyan rendszerekben, ahol a memória korlátozott, például beágyazott rendszerekben vagy pénzügyi alkalmazásokban, ahol a pontosság és a kompakt tárolás fontos.
A csomagolt BCD a memóriahasználat szempontjából hatékonyabb, míg a csomagolatlan BCD egyszerűbb feldolgozást tesz lehetővé.
A két BCD típus közötti választás a konkrét alkalmazási követelményektől függ. A csomagolatlan BCD előnye a egyszerűség. Mivel minden számjegy külön bájton van tárolva, a számjegyekhez való hozzáférés és a velük való műveletek végrehajtása egyszerűbb. A csomagolt BCD viszont a memória hatékonyságát helyezi előtérbe, ami különösen fontos lehet korlátozott erőforrásokkal rendelkező rendszerekben.
Az alábbi táblázat összefoglalja a két BCD típus közötti főbb különbségeket:
| Jellemző | Csomagolatlan BCD | Csomagolt BCD |
|---|---|---|
| Memóriahasználat | Egy számjegy egy bájt | Két számjegy egy bájt |
| Feldolgozás | Egyszerűbb | Komplexebb |
| Alkalmazási területek | Gyors feldolgozást igénylő rendszerek | Memóriakorlátozott rendszerek |
Például, ha egy egyszerű számológépet tervezünk, ahol a gyors számítás a prioritás, a csomagolatlan BCD lehet a jobb választás. Ezzel szemben, ha egy pénzügyi adatbázist hozunk létre, ahol nagy mennyiségű adatot kell tárolnunk a lehető legkisebb helyen, a csomagolt BCD a megfelelő megoldás.
A BCD számábrázolás további aspektusa a előjeles BCD, amely lehetővé teszi negatív számok ábrázolását is. Az előjeles BCD-ben egy külön bitet vagy nibble-t (4 bit) használunk az előjel tárolására. Ez a bit vagy nibble általában a szám legmagasabb helyiértékén található. Például, a 1100 nibble gyakran a pozitív előjelet, míg a 1101 a negatív előjelet jelöli. Az előjeles BCD-t gyakran használják olyan alkalmazásokban, ahol a negatív számok ábrázolása elengedhetetlen, például pénzügyi számításokban vagy mérőműszerekben.
A BCD ábrázolásának előnyei és hátrányai
A binárisan kódolt decimális (BCD) ábrázolás, bár nem a legelterjedtebb számábrázolási mód, bizonyos területeken jelentős előnyökkel rendelkezik. Az egyik legfontosabb előnye a pontos decimális ábrázolás. Míg a bináris lebegőpontos számábrázolás (mint például az IEEE 754 szabvány) bizonyos decimális törtek esetén kerekítési hibákhoz vezethet, a BCD megőrzi a decimális pontosságot. Ez különösen kritikus pénzügyi számításoknál vagy olyan alkalmazásoknál, ahol a legkisebb eltérés is elfogadhatatlan.
Egy másik jelentős előny a könnyű konverzió decimális formátumokba. Mivel minden decimális számjegy külön, binárisan van kódolva, az átváltás a decimális megjelenítéshez (például szöveges formátumba) egyszerűen elvégezhető. Ez különösen hasznos olyan rendszerekben, amelyek sok adatot jelenítenek meg a felhasználó számára, például digitális órák, számológépek vagy pénztárgépek.
A BCD egyik legfontosabb előnye a közvetlen megfelelés a decimális rendszernek, ami kiküszöböli a bináris ábrázolásból adódó kerekítési hibákat bizonyos alkalmazásokban.
Ugyanakkor a BCD-nek hátrányai is vannak. Az egyik legszembetűnőbb a kevesebb hatékonyság a tárhely kihasználásában. Míg egy 4 bites bináris szám 16 különböző értéket képes ábrázolni (0-tól 15-ig), a BCD-ben ugyanez a 4 bit csak 10 értéket (0-tól 9-ig) tud ábrázolni. Ez azt jelenti, hogy a BCD ábrázolás pazarlóbb, mint a bináris, mivel a 10-nél nagyobb értékek ábrázolására nem használja ki a rendelkezésre álló bitek teljes potenciálját. Ez különösen nagy adathalmazok esetén válhat problémássá.
Egy másik hátrány a bonyolultabb aritmetikai műveletek. A bináris számokkal való műveletek (összeadás, kivonás, szorzás, osztás) egyszerűen elvégezhetők bináris áramkörökkel. A BCD számokkal való műveletekhez azonban speciális korrekciós lépésekre van szükség, mivel a bináris összeadás eredménye nem feltétlenül érvényes BCD számjegy. Például, ha két BCD számjegyet adunk össze, és az eredmény nagyobb, mint 9, akkor 6-ot kell hozzáadnunk az eredményhez, hogy korrigáljuk a decimális átvitelt. Ez a bonyolultság növeli a hardverigényt és a számítási időt.
Végül, a BCD kevésbé elterjedt, mint a bináris ábrázolás. Ez azt jelenti, hogy kevesebb eszköz és könyvtár áll rendelkezésre a BCD számokkal való munkához, ami megnehezítheti a fejlesztést és a hibakeresést. Mindazonáltal, a BCD továbbra is releváns bizonyos speciális alkalmazásokban, ahol a pontosság és a könnyű konverzió fontosabb, mint a tárhely hatékonysága és a számítási sebesség.
A BCD és a bináris számrendszer összehasonlítása
A binárisan kódolt decimális (BCD) egy olyan számábrázolási módszer, amely a decimális számrendszer számjegyeit bináris számokkal fejezi ki. Ezzel szemben a hagyományos bináris számrendszer (más néven kettes számrendszer) egy adott számot kettes alapú hatványok összegeként reprezentálja. A BCD lényege, hogy minden decimális számjegyet (0-tól 9-ig) külön-külön kódol, általában 4 biten.
A BCD és a bináris számrendszer közötti egyik fő különbség az ábrázolási hatékonyság. Míg a bináris rendszer hatékonyabban használja ki a biteket (kevesebb bit szükséges egy adott érték ábrázolásához), a BCD könnyebben olvasható és konvertálható az emberek számára, akik a decimális számrendszerhez vannak szokva. Például, a 15 decimális szám binárisan 1111, BCD-ben pedig 0001 0101. Látható, hogy BCD-ben több bitre van szükség.
A BCD-t gyakran használják olyan alkalmazásokban, ahol a pontos decimális ábrázolás elengedhetetlen, például pénzügyi rendszerekben. A bináris rendszerben a lebegőpontos számok ábrázolása kerekítési hibákhoz vezethet, ami elfogadhatatlan a pénzügyi számításoknál. A BCD használatával ezek a hibák elkerülhetők, mivel a decimális számjegyek közvetlenül vannak ábrázolva.
A bináris számrendszer a számítógépek belső működéséhez ideális, míg a BCD a felhasználói felületek és a külső adattárolás szempontjából előnyösebb.
A matematikai műveletek végrehajtása is eltér a két rendszerben. Bináris számokon a műveletek közvetlenül a bináris logikával végezhetők el. BCD-ben viszont speciális korrekciós lépésekre van szükség, mivel a 4 bites csoportok csak a 0-9 tartományban érvényesek. Például, ha két BCD számjegy összege nagyobb, mint 9, akkor hozzá kell adni 6-ot (0110 binárisan) a korrekcióhoz.
Nézzük a következő példát: Adjuk össze a 17 és 25 decimális számokat BCD-ben.
- 17 BCD-ben: 0001 0111
- 25 BCD-ben: 0010 0101
- Összeadás: 0001 0111 + 0010 0101 = 0011 1100
- A 1100 érvénytelen BCD kód, ezért hozzáadjuk a 0110-at: 1100 + 0110 = 1 0010
- Az eredmény: 0100 0010, ami 42 decimálisan.
A bináris számrendszer hatékonyabb tárolást tesz lehetővé, míg a BCD egyszerűbb konverziót és pontosabb decimális ábrázolást kínál, különösen a pénzügyi és más, pontosságot igénylő alkalmazásokban. A választás a konkrét alkalmazási területtől függ.
A BCD konverziója bináris és decimális számok között
A binárisan kódolt decimális (BCD) egy olyan számábrázolási rendszer, amelyben minden decimális számjegyet külön-külön bináris számokkal kódolunk. Gyakran 4 bitet használunk egy decimális számjegy ábrázolására, ami lehetővé teszi a 0-tól 9-ig terjedő számjegyek kódolását. A BCD elsődleges célja, hogy megkönnyítse a decimális adatok tárolását és feldolgozását a számítógépes rendszerekben, különösen olyan alkalmazásokban, ahol a pontos decimális ábrázolás kritikus, például pénzügyi számításoknál.
A BCD konverziója bináris és decimális számok között kétirányú folyamat. A decimális-BCD konverzió során minden decimális számjegyet a megfelelő 4-bites bináris kódra alakítunk. Például a 29 decimális szám BCD formában 0010 1001 lesz, ahol 0010 a 2-t, és 1001 a 9-et reprezentálja. Ez a konverzió viszonylag egyszerű, mert a decimális számjegyek közvetlenül leképezhetők a megfelelő bináris kódjukra.
A BCD-decimális konverzió a fordított folyamat, ahol a BCD számjegyet a megfelelő decimális számjeggyé alakítjuk. Ebben az esetben minden 4-bites csoportot megvizsgálunk, és a hozzá tartozó decimális számjeggyé alakítjuk. Ha egy 4-bites csoport nem érvényes BCD kód (azaz nagyobb, mint 9), akkor hibát jelezhetünk, vagy speciális kezelést alkalmazhatunk. Fontos megjegyezni, hogy a BCD nem használja ki teljesen a 4 bit adta lehetőségeket (16 különböző érték), mivel csak a 0-9 közötti értékeket ábrázolja.
A bináris-BCD konverzió bonyolultabb, mert először a bináris számot decimálissá kell alakítani, majd a decimális számot BCD formátumra konvertálni. Például, ha a 110010 bináris számot (ami 50 decimálisan) BCD-re szeretnénk konvertálni, először decimálissá alakítjuk (50), majd a 5-öt és a 0-t külön-külön BCD-re alakítjuk, ami 0101 0000 lesz.
A BCD-bináris konverzió még bonyolultabb, mert a BCD számot először decimálissá kell alakítani, majd a decimális számot binárissá. Például a 0001 0001 BCD szám (ami 11 decimálisan) esetén először decimálissá alakítjuk (11), majd a 11-et binárissá konvertáljuk, ami 1011 lesz.
A BCD használata egyszerűsíti a decimális aritmetikát a számítógépekben, különösen a pénzügyi rendszerekben, ahol a kerekítési hibák minimalizálása elengedhetetlen.
A BCD előnye, hogy megőrzi a decimális pontosságot, elkerülve a lebegőpontos számábrázolásból adódó kerekítési hibákat. Hátránya viszont, hogy kevésbé hatékonyan használja a memóriát, mint a bináris ábrázolás, mivel minden decimális számjegyhez 4 bitre van szükség, még akkor is, ha a bináris ábrázolás kevesebb bitet igényelne. Továbbá, a BCD aritmetikai műveletek bonyolultabbak lehetnek, mint a bináris aritmetika.
Számos módszer létezik a BCD számok tárolására. A leggyakoribb a csomagolt BCD, ahol két decimális számjegyet tárolunk egyetlen byte-ban (8 bit). Ezzel a módszerrel hatékonyabban használhatjuk a memóriát, mint a csomagolatlan BCD, ahol minden decimális számjegyet külön byte-ban tárolunk. A csomagolatlan BCD használata egyszerűbb aritmetikai műveleteket tesz lehetővé, de több memóriát igényel.
A BCD-t gyakran használják digitális órákban és számológépekben, mert egyszerűen megjeleníthetők a decimális kijelzőkön. Az ilyen eszközökben a BCD használata egyszerűsíti a számok megjelenítését és a decimális aritmetikai műveletek végrehajtását.
A BCD használata során figyelembe kell venni a BCD aritmetikai műveletek sajátosságait. Például a BCD összeadás során, ha az eredmény nagyobb, mint 9, akkor 6-ot kell hozzáadni az eredményhez, hogy érvényes BCD számjegyet kapjunk. Ez a korrekciós lépés biztosítja, hogy az eredmény továbbra is megfeleljen a BCD formátumnak.
A BCD konverziója és használata megköveteli a megfelelő algoritmusok és rutinok ismeretét, valamint a BCD ábrázolás sajátosságainak megértését. A helyes implementáció elengedhetetlen a pontos és megbízható decimális aritmetika eléréséhez.
A BCD aritmetikai műveletei: összeadás, kivonás, szorzás, osztás

A binárisan kódolt decimális (BCD) számokkal végzett aritmetikai műveletek – összeadás, kivonás, szorzás és osztás – speciális eljárásokat igényelnek, mivel a BCD nem egy natív bináris ábrázolás. Az alapelv az, hogy minden decimális számjegyet külön-külön kezelünk, és a műveleteket úgy végezzük el, hogy az eredmény továbbra is érvényes BCD formátumban maradjon.
BCD összeadás: A BCD összeadás során a decimális számjegyeket külön-külön adjuk össze, mintha bináris számok lennének. Ha az összeg nagyobb, mint 9 (1001 binárisan), akkor az eredmény érvénytelen BCD számjegy. Ebben az esetben 6-ot (0110 binárisan) hozzá kell adni az eredményhez, hogy az érvényes BCD formátumba kerüljön, és a következő decimális helyiértékre átvitelt (carry) kell generálni. Például:
- Ha 5 + 3 = 8, akkor az eredmény érvényes BCD.
- Ha 7 + 5 = 12 (binárisan 1100), ez érvénytelen BCD. Hozzáadunk 6-ot: 1100 + 0110 = 10010. Ekkor az eredmény 2 (0010) lesz, és 1 átvitel (carry) keletkezik.
BCD kivonás: A BCD kivonás hasonló az összeadáshoz, de itt a probléma az, hogy ha az alsó számjegy nagyobb, mint a felső, akkor kölcsön kell venni a következő decimális helyiértékről. Ha a kivonás eredménye negatív, akkor 10-et kell hozzáadni az eredményhez, és 1-et kölcsönvenni a következő helyiértékről. Ezután a kapott decimális számjegyhez hozzá kell adni a 1010-et (ami a 10 komplementere), hogy megkapjuk a helyes BCD eredményt. Valójában a 10-es komplemenst használjuk a kivonáshoz.
A BCD kivonás lépései:
- Végezd el a kivonást a megfelelő decimális helyiértéken.
- Ha az eredmény pozitív vagy nulla, akkor az érvényes BCD.
- Ha az eredmény negatív, akkor adj hozzá 10-et az eredményhez, és vonj ki 1-et a következő helyiértékről.
- Ha kölcsönzésre volt szükség, akkor vond ki 6-ot (0110) az eredményből, hogy korrigáld a BCD értéket.
BCD szorzás: A BCD szorzás bonyolultabb, és általában ismételt összeadással és eltolással valósítják meg. Minden egyes szorzó számjegyet külön-külön szorzunk a szorzandóval, majd a részeredményeket megfelelően eltoljuk (decimális helyiérték szerint), és összeadjuk. Az összeadásnál a fent leírt BCD összeadási algoritmust kell alkalmazni. A szorzás során figyelni kell az átvitelekre és a helyes BCD formátum megtartására.
A BCD szorzás lépései:
- Szorozd meg a szorzandót a szorzó minden egyes számjegyével.
- Minden részeredményt tol el a megfelelő helyiértékre.
- Add össze a részeredményeket BCD összeadással.
BCD osztás: A BCD osztás a legbonyolultabb művelet. Gyakran ismételt kivonással és eltolással valósítják meg. A lényeg, hogy a BCD osztás során a maradékot és a hányadost is BCD formátumban kell tartani. Az osztás során folyamatosan ellenőrizni kell, hogy a kivonás eredménye érvényes BCD-e, és szükség esetén korrekciókat kell végrehajtani.
A BCD osztás lépései:
- Állítsd be az osztandót és az osztót.
- Ismételten vond ki az osztót az osztandóból (vagy a részleges osztandóból), amíg az eredmény negatív nem lesz.
- Számold meg, hányszor sikerült kivonni az osztót (ez a hányados egy számjegye).
- Korrigáld a maradékot (ha negatív lett).
- Tol el az osztandót (vagy a maradékot) a következő helyiértékre, és ismételd a folyamatot.
A BCD aritmetikai műveletek során a legfontosabb a decimális számjegyek integritásának megőrzése, és a megfelelő korrekciók elvégzése minden egyes lépésben.
A BCD aritmetikai műveletek implementálása általában több erőforrást igényel, mint a bináris aritmetika, de a decimális számokkal való közvetlen munkavégzés pontosságot biztosít, különösen olyan alkalmazásokban, mint a pénzügyi számítások, ahol a kerekítési hibák elfogadhatatlanok.
A BCD használata számológépekben, digitális órákban és más olyan rendszerekben elterjedt, ahol a decimális formátumú adatokkal való közvetlen munkavégzés előnyös.
A BCD alkalmazásai a gyakorlatban: órák, számológépek, pénzügyi rendszerek
A binárisan kódolt decimális (BCD) egy számábrázolási módszer, melyben minden decimális számjegyet külön-külön bináris kóddal reprezentálunk. Ahelyett, hogy egy teljes számot bináris formátumba konvertálnánk, a BCD a decimális számjegyeket tartja meg, ezzel megkönnyítve az emberek számára olvasható formátumokba történő konvertálást és visszaalakítást. Ez a tulajdonság különösen hasznos a különböző alkalmazásokban, ahol a pontos decimális ábrázolás és a könnyű megjeleníthetőség kritikus szempont.
A BCD széles körben elterjedt a gyakorlati alkalmazásokban, különösen azokban az eszközökben és rendszerekben, ahol a decimális számok pontos megjelenítése és kezelése elengedhetetlen. Nézzünk meg néhány konkrét példát:
Órák és időzítők: A digitális órák és időzítők gyakran használják a BCD-t az idő megjelenítésére. Mivel az idő értékek (órák, percek, másodpercek) decimálisak (0-59, 0-23), a BCD lehetővé teszi, hogy az egyes számjegyeket közvetlenül vezéreljék a kijelzőn. Ez leegyszerűsíti a hardveres és szoftveres tervezést, mivel nincs szükség bonyolult bináris-decimális konverziókra a megjelenítéshez.
Számológépek: A zsebszámológépek és egyéb számítási eszközök gyakran alkalmazzák a BCD-t a decimális számok pontos ábrázolására és kezelésére. A lebegőpontos számábrázolással szemben, amely kerekítési hibákhoz vezethet, a BCD pontos decimális aritmetikát tesz lehetővé, ami különösen fontos a pénzügyi számításoknál és más olyan alkalmazásokban, ahol a pontosság kritikus.
Pénzügyi rendszerek: A banki rendszerek, pénztárgépek és más pénzügyi alkalmazások szinte kivétel nélkül a BCD-t használják a pénzösszegek ábrázolására. Ennek oka, hogy a pénzügyi tranzakciók során a legkisebb kerekítési hiba is jelentős anyagi veszteséghez vezethet. A BCD biztosítja, hogy a pénzügyi számítások pontosak és megbízhatóak legyenek, elkerülve a kerekítési hibákból adódó eltéréseket.
A pénzügyi rendszerekben a BCD használata nem csak a pontosság miatt fontos, hanem a szabályozási követelmények miatt is. Sok országban a pénzügyi szoftvereknek meg kell felelniük bizonyos szabványoknak, amelyek előírják a pontos decimális aritmetika használatát. A BCD megfelel ezeknek a követelményeknek, és segít a pénzügyi intézményeknek a szabályozások betartásában.
A BCD előnyei ellenére fontos megjegyezni, hogy a bináris ábrázoláshoz képest több memóriát igényelhet, mivel nem használja ki teljesen a bináris kódolás kapacitását. Például, egy 4-bites BCD kód csak 0-9 közötti számjegyeket ábrázol, míg egy 4-bites bináris kód 0-15 közötti értékeket tud tárolni.
Azonban a pontosság és a könnyű decimális konverzió előnyei gyakran felülmúlják ezt a hátrányt azokban az alkalmazásokban, ahol a decimális számok pontos kezelése elengedhetetlen.
Összességében a BCD egy értékes eszköz a számítástechnikában, különösen azokban az alkalmazásokban, ahol a decimális számok pontos ábrázolása és kezelése kritikus szempont. Az órák, számológépek és pénzügyi rendszerek csak néhány példa arra, hogy a BCD hogyan biztosítja a megbízható és pontos decimális aritmetikát a mindennapi életünkben.
Hibakezelés és korrekció BCD aritmetikában
A BCD aritmetika, bár egyszerűbb decimális számításokat tesz lehetővé a bináris rendszerekben, nem mentes a hibáktól. A hibák forrása többféle lehet, beleértve a kerekítési hibákat, a túllépéseket és a helytelen BCD kódolást.
A kerekítési hibák különösen akkor jelentkeznek, ha a BCD számokkal történő osztás nem ad pontos decimális eredményt. Mivel a BCD ábrázolás csak a decimális számjegyeket tárolja, a tört részeket le kell kerekíteni vagy csonkítani, ami információvesztéshez vezet. Ennek minimalizálására nagyobb pontosságú BCD ábrázolást (több decimális jegyet) használhatunk, vagy speciális kerekítési algoritmusokat alkalmazhatunk.
A túllépés akkor következik be, amikor a művelet eredménye meghaladja a rendelkezésre álló BCD számjegyek számát. Például, ha egy 4 jegyű BCD számot használunk, a maximális ábrázolható érték 9999. Ha az eredmény ennél nagyobb, túllépés történik. A túllépés kezelésére többféle módszer létezik. Az egyik lehetőség a túllépés jelző használata, amely jelzi, ha túllépés történt. Egy másik lehetőség a nagyobb BCD ábrázolás használata, amely több számjegyet képes tárolni.
A helytelen BCD kódolás akkor fordul elő, ha egy számjegy bináris ábrázolása nem érvényes BCD kód. A BCD kódok 0-tól 9-ig terjednek (0000-tól 1001-ig). A 1010-től 1111-ig terjedő kódok érvénytelenek. Ha egy ilyen érvénytelen kód kerül a számításba, az hibás eredményhez vezethet. A helytelen BCD kódolás elkerülése érdekében ellenőrizni kell a bemeneti adatokat és helyes BCD konverziós rutinokat kell használni.
A BCD aritmetikában a hibakezelés és korrekció kritikus fontosságú a megbízható és pontos eredmények biztosításához.
A hibák észlelésére és korrekciójára különböző technikák léteznek. Ezek közé tartozik:
- Validációs ellenőrzések: A bemeneti adatok ellenőrzése annak biztosítására, hogy érvényes BCD kódokat tartalmaznak.
- Paritás ellenőrzés: A paritás bit hozzáadása minden BCD számjegyhez a hibák észleléséhez.
- Hibajavító kódok: Komplexebb kódok használata a hibák észlelésére és javítására.
- Redundancia: Ugyanazon számítás többszöri elvégzése és az eredmények összehasonlítása a hibák azonosítására.
A BCD aritmetika, bár robusztus, gondos tervezést és implementációt igényel a hibák minimalizálása érdekében. A megfelelő hibakezelési és korrekciós technikák alkalmazásával biztosíthatjuk a BCD számítások pontosságát és megbízhatóságát.
A BCD aritmetikai műveletek során, például összeadásnál, ha az eredmény egy adott számjegy pozícióban nagyobb, mint 9 (1001), akkor 6-ot (0110) kell hozzáadni az eredményhez, hogy a megfelelő BCD formátumot megkapjuk. Ezt a korrekciós lépést elhanyagolva hibás eredményt kapunk. Hasonló korrekciókra van szükség kivonásnál is, ha „kölcsönzésre” van szükség.
A BCD aritmetika alkalmazásakor a programozónak vagy a tervezőnek expliciten kell kezelnie ezeket a korrekciós lépéseket, mivel a legtöbb általános célú processzor nem támogatja natívan a BCD aritmetikát. A hibakezelés és a korrekciós mechanizmusok implementálása növeli a kód komplexitását, de elengedhetetlen a pontos eredmények eléréséhez olyan alkalmazásokban, mint például a pénzügyi számítások vagy a mérési rendszerek.
A BCD kódolásának optimalizálása
A binárisan kódolt decimális (BCD) egy számábrázolási rendszer, ahol minden decimális számjegyet külön-külön binárisan kódolunk. A hagyományos BCD esetében ez 4 bitet jelent számjegyenként, ami lehetővé teszi a 0-tól 9-ig terjedő értékek ábrázolását. Azonban a BCD kódolásának hatékonysága és optimalizálása különböző szempontok mentén történhet.
Az egyik optimalizációs lehetőség a tömörített BCD (packed BCD) használata. Ebben az esetben két decimális számjegyet tárolunk egyetlen byte-ban (8 bit). Ezáltal a memória kihasználtság jelentősen javul, különösen akkor, ha nagy mennyiségű decimális adatot kell tárolni. Például, a 1234-es számot a hagyományos BCD-ben 16 biten tárolnánk, míg tömörített BCD-ben 8 biten.
A zónázott decimális (zoned decimal) egy másik variáns, amely leginkább az IBM nagyszámítógépeknél volt elterjedt. Itt minden számjegyhez egy külön byte tartozik, a felső 4 bit a „zóna” (általában F hexadecimális érték), az alsó 4 bit pedig a decimális számjegyet ábrázolja. Az utolsó byte-ban a zóna helyén a szám előjele található.
A BCD aritmetikai műveletek (összeadás, kivonás) speciális korrekciós lépéseket igényelnek, mivel a bináris összeadó nem kezeli a decimális túlcsordulást automatikusan.
A BCD kódolás előnye a pontos decimális ábrázolás, elkerülve a lebegőpontos számok ábrázolásából adódó kerekítési hibákat. Ez különösen fontos pénzügyi vagy más, nagy pontosságot igénylő alkalmazásokban. Azonban hátránya, hogy kevésbé hatékony a memória kihasználtsága és a számítási sebessége, mint a bináris ábrázolás.
Az optimalizálás során figyelembe kell venni a konkrét alkalmazási területet. Ha a memória korlátozott, a tömörített BCD lehet a megfelelő választás. Ha a sebesség kritikus, akkor a bináris ábrázolás és konverzió lehet hatékonyabb, bár ekkor a kerekítési hibákkal számolni kell.
BCD implementáció hardverben és szoftverben
A BCD (Binary-Coded Decimal) implementációja hardverben és szoftverben eltérő megközelítéseket igényel. Hardveres szinten a BCD használata egyszerűsítheti a decimális aritmetikai műveleteket végző áramkörök tervezését. Például, egy BCD összeadó közvetlenül tudja kezelni a decimális számjegyeket, anélkül, hogy bináris konverzióra lenne szükség.
Szoftveres környezetben a BCD használata gyakran memória-hatékonysági okokból indokolt, különösen olyan rendszerekben, ahol a memória korlátozott. A BCD lehetővé teszi a decimális számok pontos tárolását és kezelését, elkerülve a lebegőpontos számábrázolásból adódó kerekítési hibákat.
A BCD széles körben alkalmazzák pénzügyi és számviteli rendszerekben, ahol a pontosság kritikus fontosságú.
A BCD implementációjának szoftveres megvalósítása különböző módszerekkel történhet. Például, használhatók speciális BCD aritmetikai függvények, amelyek a decimális műveleteket bináris műveletekre bontják, majd a végeredményt BCD formátumra alakítják vissza. Egyes programozási nyelvek, mint például a COBOL, natív támogatást nyújtanak a BCD-hez.
Bár a BCD egyszerűsítheti a decimális számok kezelését, a bináris ábrázoláshoz képest kevésbé hatékony a memória kihasználása szempontjából, mivel minden decimális számjegyhez 4 bit szükséges, ami pazarlás, ha a nagyobb számok binárisan ábrázolhatók kevesebb bittel.


